История развития математического образования на кафедре «Высшая математика»
 Становление научной школы математики в МГТУ им. Н.Э. Баумана связано с именем Алексея Васильевича Летникова (1837-1888), возглавившего в 1868 г. кафедру высшей математики и аналитической механики, созданную при преобразовании Московского ремесленного учебного заведения в Императорское Московское техническое училище. В 1878 г. из состава этой кафедры выделилась кафедра высшей математики, которой А.В.Летников продолжал руководить до конца своей жизни.
Становление научной школы математики в МГТУ им. Н.Э. Баумана связано с именем Алексея Васильевича Летникова (1837-1888), возглавившего в 1868 г. кафедру высшей математики и аналитической механики, созданную при преобразовании Московского ремесленного учебного заведения в Императорское Московское техническое училище. В 1878 г. из состава этой кафедры выделилась кафедра высшей математики, которой А.В.Летников продолжал руководить до конца своей жизни.
А.В.Летников родился в Москве, окончил здесь гимназию и Межевой институт, был в течение двух лет вольнослушателем Московского университета, а затем три года слушал лекции крупных французских математиков Серре, Шаля, Бертрана, Лиувилля, Пьюизе и других в парижской Политехнической школе при Сорбонне. В 1860 г. он вернулся в Москву и начал читать курс теории вероятностей в Межевом институте.
В первом томе «Математического сборника» (1866) А.В.Летников опубликовал свою первую научную работу по теории дифференциальных уравнений, в том числе уравнения Риккати. В 1867 г. ему была присуждена степень доктора Лейпцигского университета по теории дифференциальных уравнений. Международное признание дало ему право без университетского диплома сдать магистерские экзамены, а затем и успешно защитить магистерскую диссертацию на тему «Теория дифференцирования с произвольным указателем».
Идеи магистерской диссертации А.В. Летникова «Теория дифференцирования с произвольным указателем» были в дальнейшем развиты им в докторской диссертации «Исследования, относящиеся к теории интегралов вида
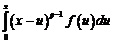
напечатанной в «Математическом сборнике» (т. 7, 1874 г.). При помощи предложенной им теории дифференцирования с дробным показателем ему удалось создать новый метод анализа особенностей решений обыкновенного дифференциального уравнения
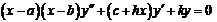
которое обобщает важные классы дифференциальных уравнений: гипергеометрическое, Бесселя, уравнения многочленов Лежандра и Чебышева. В 1882-1885 гг. в тт. 10-12 «Математического сборника» он опубликовал статьи о модификации этого метода применительно к сферическим функциям. Научные труды А.В.Летникова заслужили всеобщее признание, что было подтверждено избранием его членом-корреспондентом Петербургской академии наук.
Идеи А.В.Летникова в работах этого цикла непосредственно перекликались с идеями магистерской диссертации М.Е.Ващенко-Захарченко «Символическое исчисление и приложение его к интегрированию линейных дифференциальных уравнений» (1862 г., Киев) об упрощении решения дифференциальных и разностных уравнений. Серия работ английского ученого О.Хевисайда по применению операционного исчисления к решению электротехнических задач была начата лишь в 1887 г., причем в этих работах использовались подходы, сходные с идеями М.Е.Ващенко-Захарченко и А.В.Летникова, но без достаточно строгого математического обоснования. Научная работа А.В.Летникова была тесно связана с его педагогической деятельностью, что сыграло важную роль в математической подготовке инженеров в училище. Сложился характерный для А.В.Летникова стиль чтения лекций: простота, ясность при одновременной оригинальности математических доказательств.
Программа курса математики для различных отделений училища в то время включала аналитическую геометрию, анализ, сферическую геометрию, начала дифференциальной геометрии и высшей алгебры. Из специальных курсов выделялся прочитанный А.В.Летниковым курс вариационного исчисления, позднее вышедший отдельным изданием. Он был автором руководств по общим разделам анализа — дифференциальному и интегральному исчислению и их приложениям, дифференциальным уравнениям.
А.В.Летников помимо кафедры высшей математики возглавлял в училище и комиссию по разработке общей системы теоретической и практической подготовки инженеров, получившей всемирную известность как «русский метод обучения ремеслам», преподавал математику в Межевом институте, а с 1883 г. был директором Московского коммерческого училища. Будучи одним из инициаторов создания и учредителей Московского математического общества, ученый сделал на его заседаниях 15 докладов, материалы которых печатались в выпускаемом этим обществом «Математическом сборнике». В частности, в т. 3 этого сборника (1868) он впервые опубликовал на русском языке в своем переводе с немецкого одну из определяющих работ Н.И.Лобачевского «Геометрические основания теории параллельных». В предисловии к этой публикации А.В.Летников по достоинству оценил революционный переворот в геометрии, осуществленный Н.И.Лобачевским, и в дальнейшем в числе немногих русских математиков настойчиво пропагандировал его идеи. По инициативе А.В.Летникова в «Математическом сборнике» был создан специальный раздел по вопросам методики преподавания математики, причем не только высшей, но и элементарной. В этом разделе он напечатал несколько статей методического характера. Этим же вопросам была посвящена его речь «О системах реального образования», произнесенная им в ИМТУ в 1871 г. во время ежегодной торжественной церемонии выпуска студентов.
 С 1872 г. начал свою работу в училище в должности преподавателя математики выдающийся русский ученый-механик, создатель кафедры теоретической механики в ИМТУ Николай Егорович Жуковский (1847-1921), который своими математическими исследованиями оказал влияние на развитие научной школы математики, в том числе в области качественной теории дифференциальных уравнений.
С 1872 г. начал свою работу в училище в должности преподавателя математики выдающийся русский ученый-механик, создатель кафедры теоретической механики в ИМТУ Николай Егорович Жуковский (1847-1921), который своими математическими исследованиями оказал влияние на развитие научной школы математики, в том числе в области качественной теории дифференциальных уравнений.
В своей магистерской диссертации «Кинематика жидкого тела», опубликованной в т. 8 «Математического сборника» (1876), при рассмотрении некоторых случаев плоскопараллельного движения несжимаемой жидкости он ввел классификацию особых точек дифференциальных уравнений первого порядка, которая содержала все четыре основных вида особых точек («узел», «седло», «фокус», «центр»), систематизированных затем в работах одного из признанных создателей качественной теории дифференциальных уравнений французского математика А.Пуанкаре.
Н.Е.Жуковский также исследовал поведение интегральных кривых в окрестности особой точки каждого вида. Однако это направление исследований, являвшееся лишь ответвлением его работ по механике, в дальнейшем не получило продолжения. Но авторитет Н.Е.Жуковского в развитии качественной теории дифференциальных уравнений был настолько высок, что в 1892 г. он выступил в Московском университете оппонентом на защите А.М.Ляпуновым докторской диссертации «Общая задача об устойчивости движения», в значительной мере определившей основные идеи и методы последующих работ в этой области.
Глубокая и взаимно обогащающая связь научных исследований по математике и механике, ярко проявившаяся в работах Н.Е.Жуковского, была характерна для научных школ этих направлений. Например, решение им задачи определения гидродинамических сил, в том числе подъемной силы при обтекании крыла воздушным потоком, в значительной мере повлияло на развитие разделов теории функций комплексного переменного, связанных с методами конформных отображений. Следует отметить, что за работу «О прочности движения» Н.Е.Жуковский в 1882 г. получил ученую степень доктора прикладной математики. Признанием авторитета Н.Е.Жуковского в области математики явилось избрание его в 1905 г. президентом Московского математического общества, постоянным членом которого он состоял с 1876 г.
 Преподававший в ИМТУ в 1896-1906 гг. на кафедре теоретической механики его ученик, один из основоположников современной гидроаэродинамики, академик Сергей Алексеевич Чаплыгин (1869-1942) разработал приближенный метод интегрирования обыкновенных дифференциальных уравнений первого порядка и их систем, вошедший затем в математическую литературу под названием метода Чаплыгина.
Преподававший в ИМТУ в 1896-1906 гг. на кафедре теоретической механики его ученик, один из основоположников современной гидроаэродинамики, академик Сергей Алексеевич Чаплыгин (1869-1942) разработал приближенный метод интегрирования обыкновенных дифференциальных уравнений первого порядка и их систем, вошедший затем в математическую литературу под названием метода Чаплыгина.
В 1896 году начал свою работу на кафедре Евгений Александрович Болотов (1870-1922), известный математик и механик, выпускник Казанского университета. Его научные исследования относятся главным образом к аналитической механике. В 1907 г. Е.А. Болотов был утвержден в степени магистра прикладной математики за работу на тему «О движении материальной плоской фигуры, стесненной связями с трением». В своем отзыве на эту работу Н.Е. Жуковский отметил, что главная заслуга Болотова в этой работе – его геометрический анализ.
 Самой значительной работой Болотова по аналитической механике является его исследование наиболее общего вариационного принципа механики – принципа наименьшего принуждения Гаусса. Е.А. Болотову принадлежит обобщение принципа наименьшего принуждения, которое легло в основу дальнейших исследований этого принципа учеными казанской школы механики. Представляют также интерес работы Болотова по гидромеханике и учебные руководства по курсам математического анализа и аналитической геометрии, которые ученый много лет читал в Московском техническом училище. В училище он читал курс аналитической геометрии и одновременно вел упражнения по теоретической и аналитической механике, которую читал Н.Е. Жуковский.
Самой значительной работой Болотова по аналитической механике является его исследование наиболее общего вариационного принципа механики – принципа наименьшего принуждения Гаусса. Е.А. Болотову принадлежит обобщение принципа наименьшего принуждения, которое легло в основу дальнейших исследований этого принципа учеными казанской школы механики. Представляют также интерес работы Болотова по гидромеханике и учебные руководства по курсам математического анализа и аналитической геометрии, которые ученый много лет читал в Московском техническом училище. В училище он читал курс аналитической геометрии и одновременно вел упражнения по теоретической и аналитической механике, которую читал Н.Е. Жуковский.
В лекциях по аналитической геометрии Болотов излагал аналитическую геометрию на плоскости и в пространстве, а также сферическую тригонометрию, увязывая многие разделы этого курса с отдельными вопросами теоретической механики и астрономии.
Е.А. Болотов уделял большое внимание подготовке своих лекций. Он обрабатывал их настолько детально и тщательно, что при издании их почти не требовалось редактировать.
С 1914 по 1921 гг. Е.А. Болотов заведовал кафедрой теоретической механики Казанского университета, а в 1921-1922 – кафедрой теоретической механики ИМТУ.
 На формирование научной школы математики в училище не могла не оказать влияния деятельность выдающегося русского математика и механика академика Пафнутия Львовича Чебышева (1821-1894), у которого с преподавателями училища были давние дружеские отношения, несмотря на то, что научная жизнь ученого была связана главным образом с Санкт-Петербургом. В отчете училища за 1871 г. впервые была опубликована его работа «О центробежном уравнителе», которая явилась первым фундаментальным исследованием по теории регуляторов. В статье «О зубчатых колесах», напечатанной в 1872 г. в сборнике «Отчет и речи, произнесенные в торжественном собрании Императорского Московского технического училища 22 сентября 1872 года», он изложил аналитический метод расчета зубчатого зацепления.
На формирование научной школы математики в училище не могла не оказать влияния деятельность выдающегося русского математика и механика академика Пафнутия Львовича Чебышева (1821-1894), у которого с преподавателями училища были давние дружеские отношения, несмотря на то, что научная жизнь ученого была связана главным образом с Санкт-Петербургом. В отчете училища за 1871 г. впервые была опубликована его работа «О центробежном уравнителе», которая явилась первым фундаментальным исследованием по теории регуляторов. В статье «О зубчатых колесах», напечатанной в 1872 г. в сборнике «Отчет и речи, произнесенные в торжественном собрании Императорского Московского технического училища 22 сентября 1872 года», он изложил аналитический метод расчета зубчатого зацепления.
В последующие годы П.Л.Чебышев регулярно посещал училище, чтобы руководить изготовлением и испытаниями в механической лаборатории спроектированных им регуляторов и других механизмов и устройств. Стремление усовершенствовать шарнирный механизм, называемый параллелограммом Уатта, натолкнуло его на постановку проблемы наилучшего приближения функций, заложившей основы глубокой математической теории, значение которой оказалось существенно шире первоначальной прикладной задачи. Ему принадлежит полушутливое высказывание о взаимосвязи теории и практики: «Математика пережила ранее два периода. В первом задачи ставились богами (делосская задача об удвоении куба), во втором — полубогами (Б.Паскаль, П.Ферма). Мы вошли теперь в третий период — задачи ставит нужда (практика), причем чем задача труднее, тем плодотворнее должны быть математические методы ее решения и тем шире область их последующего применения».
 Отмеченная связь математических исследований с работами по механике и их определенная прикладная направленность прослеживаются и на последующих этапах развития научной школы математики. В 1936-1941 гг. кафедрой высшей математики заведовал д-р техн. наук, проф. Дмитрий Юрьевич Панов (1904–1975), специалист в области вычислительной математики, известный своими трудами по численному решению дифференциальных уравнений в частных производных, по нелинейной теории упругости и вибрации непризматических стержней сложного профиля.
Отмеченная связь математических исследований с работами по механике и их определенная прикладная направленность прослеживаются и на последующих этапах развития научной школы математики. В 1936-1941 гг. кафедрой высшей математики заведовал д-р техн. наук, проф. Дмитрий Юрьевич Панов (1904–1975), специалист в области вычислительной математики, известный своими трудами по численному решению дифференциальных уравнений в частных производных, по нелинейной теории упругости и вибрации непризматических стержней сложного профиля.
 Исследования в этих направлениях применительно к расчету воздушных винтов самолетов развивали в тесном контакте с ЦАГИ сотрудники кафедры Б.П. Демидович, П.М.Риз, Б.О. Солоноуц, А.Р. Янпольский.
Исследования в этих направлениях применительно к расчету воздушных винтов самолетов развивали в тесном контакте с ЦАГИ сотрудники кафедры Б.П. Демидович, П.М.Риз, Б.О. Солоноуц, А.Р. Янпольский.
 С 1936 по 1948 гг. на кафедре работал доцент (в последствие профессор) Борис Павлович Демидович (1906-1977). Основными направлениями его научной деятельности были качественная теория обыкновенных дифференциальных уравнений, математическая физика и теория функций. В своих работах (их у него около шестидесяти) Б.П. Демидович исследовал динамические системы с интегральными инвариантами, периодические и почти периодические решения, ограниченные решения обыкновенных дифференциальных уравнений, правильные и вполне правильные дифференциальные системы, устойчивость обыкновенных дифференциальных уравнений, в частности, орбитальная устойчивость динамических систем.
С 1936 по 1948 гг. на кафедре работал доцент (в последствие профессор) Борис Павлович Демидович (1906-1977). Основными направлениями его научной деятельности были качественная теория обыкновенных дифференциальных уравнений, математическая физика и теория функций. В своих работах (их у него около шестидесяти) Б.П. Демидович исследовал динамические системы с интегральными инвариантами, периодические и почти периодические решения, ограниченные решения обыкновенных дифференциальных уравнений, правильные и вполне правильные дифференциальные системы, устойчивость обыкновенных дифференциальных уравнений, в частности, орбитальная устойчивость динамических систем.
 С 1946 по 1961 гг. на кафедре работал д.ф.-м.н., профессор Петр Михайлович Риз (1902-1990). Он занимался такими проблемами как вопросы прочности в самолетостроении, теория случайных процессов, фундаментальные проблемы теории упругости. Его работы по математике и механике всегда отличались исключительной ясностью, глубиной исследований и одновременно краткостью изложения. П.М. Риз долгое время читал лекции для аспирантов и сотрудников института по совершенно различным разделам математики и механики, как, например, «Теория случайных процессов», «Теория нелинейных колебаний», «Исследование операций», «Методы функций в гидро- и аэродинамике».
С 1946 по 1961 гг. на кафедре работал д.ф.-м.н., профессор Петр Михайлович Риз (1902-1990). Он занимался такими проблемами как вопросы прочности в самолетостроении, теория случайных процессов, фундаментальные проблемы теории упругости. Его работы по математике и механике всегда отличались исключительной ясностью, глубиной исследований и одновременно краткостью изложения. П.М. Риз долгое время читал лекции для аспирантов и сотрудников института по совершенно различным разделам математики и механики, как, например, «Теория случайных процессов», «Теория нелинейных колебаний», «Исследование операций», «Методы функций в гидро- и аэродинамике».
 В 1953-1958 гг. кафедру возглавлял д-р техн. наук, проф. Кирилл Петрович Станюкович (1916-1989), выдающийся физик-теоретик, астроном, газодинамик, заслуженный деятель науки и техники РСФСР. Всего им опубликовано более 600 научных работ. Он занимался проблемами метеорной астрономии, кратерообразования на Луне и планетах, вопросами гравитации, космогонии и космологии. В области газовой динамики изучал неустановившиеся движения сплошной среды, взрывные явления, проблемы космической газодинамики. В области теоретической физики – теорию гравитации и элементарных частиц. Его работы сыграли заметную роль в развитии ряда научных направлений в газовой динамике, теории детонации, релятивистской механике сплошной среды.
В 1953-1958 гг. кафедру возглавлял д-р техн. наук, проф. Кирилл Петрович Станюкович (1916-1989), выдающийся физик-теоретик, астроном, газодинамик, заслуженный деятель науки и техники РСФСР. Всего им опубликовано более 600 научных работ. Он занимался проблемами метеорной астрономии, кратерообразования на Луне и планетах, вопросами гравитации, космогонии и космологии. В области газовой динамики изучал неустановившиеся движения сплошной среды, взрывные явления, проблемы космической газодинамики. В области теоретической физики – теорию гравитации и элементарных частиц. Его работы сыграли заметную роль в развитии ряда научных направлений в газовой динамике, теории детонации, релятивистской механике сплошной среды.
В 1959 г. кафедрой заведовал д-р техн. наук, проф. И.А.Паничкин, научные работы которого были посвящены вопросам обтекания тел вращения высокоскоростным воздушным потоком. Руководивший кафедрой в 1960-1965 гг. д-р техн. наук, проф. Н.К.Куликов разрабатывал методы решения систем обыкновенных дифференциальных уравнений с переменными коэффициентами, описывающих сложные динамические устройства, в том числе системы автоматического регулирования.
В 1966-1970 гг. заведующим кафедрой был д-р физ.-мат. наук, проф. Дюис Данилович Ивлев, известный своими работами по математической теории идеальной пластичности, предельному равновесию оболочек вращения и теории упрочняющегося пластического тела. Автор более 120 научных трудов, среди которых монографии «Теория идеальной пластичности», «Теория уплотняющегося пластического тела», «Метод возмущений теории упруго-пластичного тела», 30 авторских свидетельств на изобретения.
Высокий уровень математических исследований прикладного характера в МВТУ базировался на прочном теоретическом фундаменте, в создании которого на кафедре высшей математики училища участвовали многие видные математики, в том числе профессора Московского университета С.П. Фиников, А.Я. Хинчин, А.О. Гельфонд, Л.А.Тумаркин, работавшие в училище в сравнительно молодом возрасте, в период своего научного расцвета.
 В конце 19 – начале 20 века на кафедре работал Леонид Кузьмич Лахтин (1863-1927), российский математик, специалист в области решения алгебраических уравнений высших степеней, а также в области математической статистики. Заслуженный профессор Московского университета, ректор Московского университета (1904—1905), декан Физико-математического факультета Московского университета (1912—1918). Его магистерская диссертация «Алгебраические уравнения, разрешимые в гипергеометрических функциях» посвящена исследованию уравнений 3-й, 4-й, 5-й и одного вида 6-й степени. В 1897 году он защитил докторскую диссертацию «Дифференциальные резольвенты алгебраических уравнений высших родов».
В конце 19 – начале 20 века на кафедре работал Леонид Кузьмич Лахтин (1863-1927), российский математик, специалист в области решения алгебраических уравнений высших степеней, а также в области математической статистики. Заслуженный профессор Московского университета, ректор Московского университета (1904—1905), декан Физико-математического факультета Московского университета (1912—1918). Его магистерская диссертация «Алгебраические уравнения, разрешимые в гипергеометрических функциях» посвящена исследованию уравнений 3-й, 4-й, 5-й и одного вида 6-й степени. В 1897 году он защитил докторскую диссертацию «Дифференциальные резольвенты алгебраических уравнений высших родов».
В 1924 году Л.К. Лахтин опубликовал большой учебник по теории вероятностей.
 Известный специалист в области дифференциальной геометрии Сергей Павлович Фиников (1883-1964), работая на кафедре с 1913 г., в 1920-е годы возглавлял математическую подготовку на инженерно-строительном и электромеханическом факультетах МВТУ. Первые работы С.П. Финикова посвящены поиску главных оснований для заданного линейного элемента поверхности. Им исследовано изгибание поверхностей на кинематическом основании. Он был одним из первых геометров, перешедших в своих исследованиях на метод внешних дифференциальных форм. С.П. Фиников сыграл большую роль в распространении идей и методов Картана. В 1948 году вышла его монография «Метод внешних форм Картана», в которой наряду с изложением теории Картана, а также работ Рикье и Томаса, изложены методы определения характеристических многообразий и особых решений систем дифференциальных уравнений.
Известный специалист в области дифференциальной геометрии Сергей Павлович Фиников (1883-1964), работая на кафедре с 1913 г., в 1920-е годы возглавлял математическую подготовку на инженерно-строительном и электромеханическом факультетах МВТУ. Первые работы С.П. Финикова посвящены поиску главных оснований для заданного линейного элемента поверхности. Им исследовано изгибание поверхностей на кинематическом основании. Он был одним из первых геометров, перешедших в своих исследованиях на метод внешних дифференциальных форм. С.П. Фиников сыграл большую роль в распространении идей и методов Картана. В 1948 году вышла его монография «Метод внешних форм Картана», в которой наряду с изложением теории Картана, а также работ Рикье и Томаса, изложены методы определения характеристических многообразий и особых решений систем дифференциальных уравнений.
 В 1929-1930 гг. кафедрой высшей математики училища заведовал Александр Яковлевич Хинчин (1894-1959), один из создателей советской школы теории вероятностей, избранный в 1939 г. членом-корреспондентом АН СССР. Он перенес методы метрической теории функций в теорию чисел и теорию вероятностей, открыл закон повторного логарифма, заложил основы теории случайных процессов, разработал методы теории массового обслуживания, использовал методы теории вероятностей в качестве математического аппарата статистической физики. А.Я.Хинчин является автором ряда учебников и учебных пособий по математике, выдержавших по три-четыре издания, а «Элементарное введение в теорию вероятностей», написанное им в соавторстве с Б.В.Гнеденко, издавалось 9 раз.
В 1929-1930 гг. кафедрой высшей математики училища заведовал Александр Яковлевич Хинчин (1894-1959), один из создателей советской школы теории вероятностей, избранный в 1939 г. членом-корреспондентом АН СССР. Он перенес методы метрической теории функций в теорию чисел и теорию вероятностей, открыл закон повторного логарифма, заложил основы теории случайных процессов, разработал методы теории массового обслуживания, использовал методы теории вероятностей в качестве математического аппарата статистической физики. А.Я.Хинчин является автором ряда учебников и учебных пособий по математике, выдержавших по три-четыре издания, а «Элементарное введение в теорию вероятностей», написанное им в соавторстве с Б.В.Гнеденко, издавалось 9 раз.

В 1931 г. кафедру возглавлял Александр Осипович Гельфонд (1906-1968) — специалист в области теории чисел, теории функций комплексного переменного и конечно-разностных методов. Ему удалось установить глубокие связи между аналитическими свойствами функций комплексного переменного и теорией чисел и создать аналитические методы доказательства трансцендентности чисел. В работах 1929 г. и 1934 г. им была решена седьмая проблема Гильберта о трансцендентности чисел специального вида, а затем доказан ряд теорем о взаимной трансцендентности чисел. В теории функций ему принадлежат работы по интерполированию целых функций и связи между ростом целых функций и арифметическими свойствами их значений. В 1939 г. А.О. Гельфонд был избран членом-корреспондентом АН СССР.

В 1931-1936 гг. кафедрой заведовал Лев Абрамович Тумаркин (1904-1974). У нас в стране и за рубежом он известен своими работами в области топологии, и прежде всего по теории размерности, которые публиковались начиная с 1925 г. Одним из его наиболее важных результатов является решение поставленной П.С.Урысоном проблемы о возможности разбиения компакта n-мерным подкомпактом. Л.А. Тумаркин показал, что все основные факты теории размерности, установленные в категории компактов, справедливы и вне этой категории, поскольку найденные им доказательства не используют условий компактности, а требуют лишь метризуемости пространства и наличия в нем счетной базы.
С 1930 г. на кафедре работал, а в период 1941-1952 гг. заведовал кафедрой доктор физ.-мат. наук, проф. Адольф (Андрей) Павлович Юшкевич (1906-1993) — видный историк математики, инициатор издания трудов многих классиков математики, один из основателей и ответственный редактор сборников «Историко-математические исследования», президент Международной академии истории науки (1965-1968). Он много сделал для установления тесных научных и методических связей кафедры высшей математики МВТУ с ведущими математическими кафедрами вузов страны, что способствовало высокому уровню научных исследований и преподавания математики в училище.
 Влияние научного потенциала кафедры высшей математики на качество математической подготовки в училище и на уровень методического обеспечения математических курсов прослеживается, начиная с деятельности А.В. Летникова. В 1888 г. кафедру возглавил проф. Николай Александрович Шапошников (1851-1920), курсы лекций которого были для своего времени образцовыми, а составленные им учебные пособия долгое время являлись основными почти во всех технических вузах России. Он, как и А.В.Летников, интересовался вопросами методики преподавания элементарной математики и ее связью с методикой преподавания высшей математики. Н.А.Шапошников являлся автором ряда учебников по элементарной и высшей математике («Курс арифметики», «Основания общей арифметики и алгебры», «Основания теории детерминантов», «Курс тригонометрии», «Алгебра», «Основной курс математического анализа»), а составленный им в соавторстве с Н.К.Вальцевым «Методический сборник алгебраических задач» выдержал с 1887 г. по 1917 г. 24 издания, а после 1917 г. — еще 28 изданий.
Влияние научного потенциала кафедры высшей математики на качество математической подготовки в училище и на уровень методического обеспечения математических курсов прослеживается, начиная с деятельности А.В. Летникова. В 1888 г. кафедру возглавил проф. Николай Александрович Шапошников (1851-1920), курсы лекций которого были для своего времени образцовыми, а составленные им учебные пособия долгое время являлись основными почти во всех технических вузах России. Он, как и А.В.Летников, интересовался вопросами методики преподавания элементарной математики и ее связью с методикой преподавания высшей математики. Н.А.Шапошников являлся автором ряда учебников по элементарной и высшей математике («Курс арифметики», «Основания общей арифметики и алгебры», «Основания теории детерминантов», «Курс тригонометрии», «Алгебра», «Основной курс математического анализа»), а составленный им в соавторстве с Н.К.Вальцевым «Методический сборник алгебраических задач» выдержал с 1887 г. по 1917 г. 24 издания, а после 1917 г. — еще 28 изданий.
Одним из лучших исследований Н.А.Шапошникова является оригинальная работа «Интегрирование дифференциальных уравнений с полными дифференциалами и частными производными первого порядка», содержащая достаточно общий прием упрощения исходного уравнения и сведения его к стандартному виду. Под руководством Н.А.Шапошникова профессорами кафедры были подготовлены и изданы важнейшие курсы: «Курс аналитической геометрии» К.А.Андреева, «Анализ и аналитическая геометрия» Д.Н.Горячева, «Математический анализ» Е.А.Болотова, курсы по аналитической геометрии Л.К.Лахтина.
Вот что вспоминал об этом времени выпускник, а позднее профессор, заведующий кафедрой теоретической механики В.П.Ветчинкин: «После ухода из МТУ преподавателя Н.А.Шапошникова Е.А. Болотов занял его кафедру высшего анализа, передав кафедру аналитической геометрии заслуженному профессору К.А.Андрееву. Несмотря на это, еще долгое время основным руководством для студентов по аналитической геометрии служил литографированный курс Е.А. Болотова.»
Что касается курса математического анализа, то учебник Н.А.Шапошникова (достаточно полный, но сухой по изложению и несколько трудный для понимания) быстро был вытеснен двухтомным литографированным курсом Е.А.Болотова, который отличался оригинальностью изложения и содержал важные для практических приложений сведения — например, вывод весьма удобной формулы квадратур Понселе, которого не присутствуют ни в одном из курсов анализа других авторов, русских и иностранных, есть более 30 таких курсов — как общих, так и специально посвященных приближенным вычислениям.
В годы революции Н.А. Шапошников, уже вышедший на пенсию, оказался в Геленджике, где преподавал в женской гимназии. В сентябре 1918 он был приглашен Б.Л. Розингом в Екатеринодар (ныне Краснодар), где стал ректором только что открывшегося Северо-Кавказского политехнического института и его профессором математики. Н.А. Шапошников отстаивал сохранение СКПИ, когда над ним нависла угроза закрытия со стороны белоказачьих властей, в частности, в своей статье «Два законопроекта», опубликованной газетой «Кубанский край» (15 ноября 1918).
После 1917 г. кафедра высшей математики МВТУ играла заметную роль в организации и совершенствовании математического образования в вузах страны. В 1920-х годах при унификации в стране учебных планов подготовки инженеров-механиков по курсу высшей математики за основу был принят учебный план механического факультета МВТУ, представленный и обоснованный деканом этого факультета И.И.Куколевским. В период введения в учебный процесс всевозможных неопробированных новаций научно-педагогическая общественность училища настояла на сохранении лекционной формы обучения, в том числе по математике и другим общенаучным дисциплинам. Представители кафедры активно участвовали в многочисленных дискуссиях по проблемам преподавания математики в вузах (см., например, журналы «Естествознание и марксизм», 1930, №2,3 и «Вестник высшей школы», 1941, № 5) и последовательно отстаивали свои позиции. Научно-методические работы преподавателей кафедры регулярно публиковались в сборниках трудов, издававшихся в МВТУ.
Накопленные на кафедре в процессе преподавания методические материалы после тщательного отбора и длительной апробации использовались в многочисленных учебных пособиях для студентов. В частности, опыт ведения практических занятий по математике был обобщен в изданном в 1944 г. в МВТУ «Задачнике по высшей математике», подготовленном большим коллективом преподавателей кафедры, в который входил и погибший в декабре 1941 г. в ополчении С.Ф.Шурлапов. Этот задачник выдержал четыре издания и на его основе был составлен в 1959 г. под редакцией проф. Б.П.Демидовича сборник «Задачи и упражнения по математическому анализу для втузов». Сборник содержал более 3000 задач по всем основным разделам втузовского курса математики (за исключением аналитической геометрии) с ответами, методическими указаниями и решениями типовых примеров. Он переиздавался десять раз, был переведен на французский, испанский и португальский языки. Его авторами были преподаватели, в разное время работавшие на кафедре высшей математики МВТУ: Г.С.Бараненков, Б.П.Демидович, В.А.Ефименко, С.М.Коган, Г.Л.Лунц, Е.Ф.Поршнева, Е.П.Сычева, С.В.Фролов, Р.Я.Шостак, А.Р.Янпольский.
Длительный период методического совершенствования математической подготовки будущих инженеров в МВТУ был отражен в написанном доцентами кафедры Сергеем Васильевичем Фроловым и Родионом Яковлевичем Шостаком «Курсе высшей математики», выпущенном двумя изданиями (в 1966 г. и 1973 г.), а в 1968 г. вышло учебное пособие Р.Я.Шостака по операционному исчислению.
В 1973 г. из состава кафедры высшей математики выделилась кафедра прикладной математики, которую возглавил лауреат Государственной премии СССР д-р техн. наук, проф. Р.С.Судаков.
 Кафедру «Высшая математика» возглавил д-р физ.мат. наук, проф. Михаил Сергеевич Яров-Яровой (1929–2004) известный математическими работами в области небесной механики, математики и численного интегрирования. Он разработал аналитическую теорию полетов космического корабля к Луне, выполнил исследование движения больших планет, провел численное интегрирование уравнений движений по уточненным формулам с использованием высших производных от решения, вывел новые представления потенциала небесных тел в эллипсоидальных координатах.
Кафедру «Высшая математика» возглавил д-р физ.мат. наук, проф. Михаил Сергеевич Яров-Яровой (1929–2004) известный математическими работами в области небесной механики, математики и численного интегрирования. Он разработал аналитическую теорию полетов космического корабля к Луне, выполнил исследование движения больших планет, провел численное интегрирование уравнений движений по уточненным формулам с использованием высших производных от решения, вывел новые представления потенциала небесных тел в эллипсоидальных координатах.
Современная история кафедры «Высшая математика»
 В 1976 г. кафедру «Высшая математика» возглавил Геннадий Дмитриевич Карташов (1938–2008), заслуженный деятель науки Российской Федерации, крупный специалист в области ускоренных испытаний технических систем на надежность. Его кандидатская диссертация была посвящена решению проблемы восстановления многомерной функции распределения по ее известным маргинальным распределениям (если это возможно) или в оценке ее некоторых характеристик. В 1980 году Г.Д. Карташов защитил докторскую диссертацию «Исследование проблемы инвариантности в теории форсированных испытаний», в которой заложил основы теории ускоренных испытаний в нашей стране. Г.Д. Карташову удалось решить ряд сложных задач, возникающих в различных областях теории надёжности. В частности, им решена проблема планирования экспериментов с ненаблюдаемыми одновременно случайными величинами, проблема инвариантности в теории надёжности, установления области применимости различных моделей расходования ресурса изделий. На основе полученных теоретических результатов при помощи метода вложенных множеств Карташовым Г.Д.разработан новый подход к прогнозированию надежности изделий. В отличие от традиционного – аппроксимации реализаций изменения технических параметров по времени – предложена аппроксимация по ансамблю. Для последовательных систем, состоящих из большого количества разнотипных элементов, предложены приближенные асимптотические методы форсированных испытаний. Показано, в частности, что для дискретных систем асимптотически выполняется модель Пальмгрена-Майнера (линейного суммирования повреждений) и форсированные испытания таких систем можно проводить в рамках линейной модели, если отказы элементов полные. Г. Д. Карташов – автор более 250 работ, среди которых монографии: Г.Д.Карташов «Принципы расходования ресурса и их использование для оценки надежности» (1984); А.И.Перроте, Г.Д.Карташов, К.Н. Цветаев «Основы ускоренных испытаний радиоэлементов на надежность» (1968); Г.Д. Карташов «Ускоренные испытания элементов и систем» (1990), а также государственных стандартов. Под руководством Г.Д.Карташова было подготовлено и защищено 18 кандидатских и 4 докторских диссертаций.
В 1976 г. кафедру «Высшая математика» возглавил Геннадий Дмитриевич Карташов (1938–2008), заслуженный деятель науки Российской Федерации, крупный специалист в области ускоренных испытаний технических систем на надежность. Его кандидатская диссертация была посвящена решению проблемы восстановления многомерной функции распределения по ее известным маргинальным распределениям (если это возможно) или в оценке ее некоторых характеристик. В 1980 году Г.Д. Карташов защитил докторскую диссертацию «Исследование проблемы инвариантности в теории форсированных испытаний», в которой заложил основы теории ускоренных испытаний в нашей стране. Г.Д. Карташову удалось решить ряд сложных задач, возникающих в различных областях теории надёжности. В частности, им решена проблема планирования экспериментов с ненаблюдаемыми одновременно случайными величинами, проблема инвариантности в теории надёжности, установления области применимости различных моделей расходования ресурса изделий. На основе полученных теоретических результатов при помощи метода вложенных множеств Карташовым Г.Д.разработан новый подход к прогнозированию надежности изделий. В отличие от традиционного – аппроксимации реализаций изменения технических параметров по времени – предложена аппроксимация по ансамблю. Для последовательных систем, состоящих из большого количества разнотипных элементов, предложены приближенные асимптотические методы форсированных испытаний. Показано, в частности, что для дискретных систем асимптотически выполняется модель Пальмгрена-Майнера (линейного суммирования повреждений) и форсированные испытания таких систем можно проводить в рамках линейной модели, если отказы элементов полные. Г. Д. Карташов – автор более 250 работ, среди которых монографии: Г.Д.Карташов «Принципы расходования ресурса и их использование для оценки надежности» (1984); А.И.Перроте, Г.Д.Карташов, К.Н. Цветаев «Основы ускоренных испытаний радиоэлементов на надежность» (1968); Г.Д. Карташов «Ускоренные испытания элементов и систем» (1990), а также государственных стандартов. Под руководством Г.Д.Карташова было подготовлено и защищено 18 кандидатских и 4 докторских диссертаций.
В 1997 году было проведено еще одно разделение кафедры «Высшая математика». На ее основе была образована новая кафедра «Вычислительная математика и математическая физика», которую возглавил профессор Грешилов А. А. Кафедрой «Высшая математика» продолжал до самой смерти заведовать Карташов Г. Д.
 В 2008 году кафедру возглавил доктор технических наук, профессор Сидняев Николай Иванович. Сидняев Н.И. закончил Московский государственный технический университет им. Н.Э. Баумана, Московский государственный университет им. М.В.Ломоносова, аспирантуру при Московском государственном техническом университете им. Н.Э.Баумана и без отрыва от производства Академию народного хозяйства при Правительстве Российской Федерации. Автор более 200 научных трудов.
В 2008 году кафедру возглавил доктор технических наук, профессор Сидняев Николай Иванович. Сидняев Н.И. закончил Московский государственный технический университет им. Н.Э. Баумана, Московский государственный университет им. М.В.Ломоносова, аспирантуру при Московском государственном техническом университете им. Н.Э.Баумана и без отрыва от производства Академию народного хозяйства при Правительстве Российской Федерации. Автор более 200 научных трудов.
Сидняев Н.И. стажировался в ЦНИИМаш, ЦАГИ им. Н.Е. Жуковского, НПО им. Лавочкина, Институте Механики МГУ им. М.В. Ломоносова, Ecole Centrale de Lyon, l’Université Sorbonne (France). Занимался научно-исследовательской работой по оборонной тематике. Направления: аэромеханика, газовая динамика многофазных сред, механика жидкости газа и плазмы, прикладная механика, динамика полета и управления, прочностные расчеты, численные методы, разработка программных комплексов.
Руководил научно-исследовательскими темами и направлениями по отраслям машиностроения, авиационно-космической, металлургической и атомной промышленности (математическое моделирование, численные расчеты разработка устройств различного назначения и внедрение в производство). Работал с зарубежными и с отечественными фирмами по выполнению НИР. Работал по грантам Российского Фонда Фундаментальных Исследований (РФФИ), Минобразования и ряда ведомств. В настоящее время руководит Правительственной темой между МГТУ им. Н.Э. Баумана и ОАО «ГАЗПРОМ», по созданию комплекса новейших методик и программ, необходимых для вовлечения в разработку углеводородного сырья. Под его руководством подготовлена и разработана образовательная программа для госкорпорации «РОСНАНО». Сидняев Н.И. активно работал в рабочей группе аппарата правительства РФ. Занимался экспертизой документов для проектов Законов РФ.
 Одно из научных направлений Сидняева Н.И. – это взаимодействия газовых сред с обтекаемыми телами. В последние десятилетия эти исследования были сосредоточены в основном на двух направлениях. Первое связано с математическим моделированием обтекания высокоскостных летательных аппаратов, второе – с научными разработками в области фундаментальных проблем сверхзвуковых и гиперзвуковых течений газа. Изучены следующие проблемы: обтекание профилей дозвуковым и трансзвуковым потоком и вычисление аэродинамических коэффициентов; обтекание профиля в системе крыла и учет взаимного влияния элементов компоновки; решение обратных задач газодинамики для определения профиля по заданным распределениям нагрузки или скорости потока по его поверхности; расчет пограничного слоя в условиях ламинарно-турбулентного обтекания с вычислением точки перехода; обтекание профилей с усложненными свойствами; расчет аэродинамических характеристик различных тел при внесении конструктивных изменений и вариациях положения элементов компоновки; оптимизация профиля.
Одно из научных направлений Сидняева Н.И. – это взаимодействия газовых сред с обтекаемыми телами. В последние десятилетия эти исследования были сосредоточены в основном на двух направлениях. Первое связано с математическим моделированием обтекания высокоскостных летательных аппаратов, второе – с научными разработками в области фундаментальных проблем сверхзвуковых и гиперзвуковых течений газа. Изучены следующие проблемы: обтекание профилей дозвуковым и трансзвуковым потоком и вычисление аэродинамических коэффициентов; обтекание профиля в системе крыла и учет взаимного влияния элементов компоновки; решение обратных задач газодинамики для определения профиля по заданным распределениям нагрузки или скорости потока по его поверхности; расчет пограничного слоя в условиях ламинарно-турбулентного обтекания с вычислением точки перехода; обтекание профилей с усложненными свойствами; расчет аэродинамических характеристик различных тел при внесении конструктивных изменений и вариациях положения элементов компоновки; оптимизация профиля.
В области фундаментальных проблем высокоскоростных течений газа значительное внимание Сидняевым Н.И. уделялось вопросам совершенствования формы быстро летящих тел с целью достижения оптимальных значений аэродинамических характеристик в условиях разрушения поверхности. Сидняевым Н.И. проведены в широкие теоретические и экспериментальные исследования в области сверх- и гиперзвукового обтекания оптимальных пространственных тел, включающих изучение структуры возмущенного течения, свойств аэродинамических характеристик при различных режимах полета и наборах геометрических параметров и создание на этой основе достаточно простых и эффективных моделей расчета, позволяющих с достаточной точностью получать оценки аэродинамического сопротивления указанных тел и проводить их оптимизацию.
Теоретически в рамках модели идеальной жидкости и экспериментально с использованием различных методов, в том числе – специального оптического метода для изучения невидимых течений. В частности, теоретически обнаружены и получили экспериментальное подтверждение топологически новые структуры конических линий тока с особенностями в ударном слое при наличии маховской конфигурации ударных волн. Показано, что при их реализации нагрузка на угловую конфигурацию в окрестности режимов обтекания с плоскими ударными волнами, лежащими в плоскости передних кромок и принадлежащими на передних кромках к сильному семейству, терпит разрыв. Построены новые типы ударных волн в конических течениях с висячими скачками уплотнения, обнаруженные в эксперименте. Обнаружены режимы автоколебаний, обусловленные отрывом пограничного слоя.
Исследовано взаимодействие ударных волн с турбулентным пограничным слоем в конических течениях и его влияние на структуру течения в ударном слое и режимы обтекания. Установлена фундаментальная общность свойств отрыва турбулентного пограничного слоя в конических и плоских потоках. Построены эмпирические соотношения, позволяющие определять положение и размер области отрыва турбулентного пограничного слоя для широкого круга типов взаимодействия конических ударных волн и систем скачков уплотнения с пограничным слоем, а также прогнозировать глобальную перестройку структуры течения в конических угловых конфигурациях. Эти результаты значительно опережают соответствующие зарубежные исследования.
Определена роль каждого из параметров геометрии в снижении сопротивления сложных тел по сравнению с эквивалентными телами вращения. Определена область изменения параметров, где сложные тела обладают значительно меньшим полным сопротивлением по сравнению с эквивалентными конусами и оптимальными степенными телами вращения. Определена область ее справедливости для характерных параметров геометрии тела и различного состояния пограничного слоя, в которой модель может быть эффективно использована для постановки и решения оптимизационных задач.
Решена проблема устойчивости полета пространственных тел, с учетом известных способов стабилизации, которая потребовала изучения ряда фундаментальных вопросов: о положении центра давления пространственных тел и его зависимости от условий полета; о возможности создания компоновок, обладающих запасом статической устойчивости без использования дополнительных стабилизирующих устройств, значительно снижающих преимущество в сопротивлении по сравнению с эквивалентными телами вращения; об аэродинамике оптимальных пространственных форм при их стабилизации вращением. Впервые поставлена задача о форме конических тел в сверхзвуковом потоке, положение центра давления которых не зависит от числа Маха и угла атаки. Найдены точные и приближенные решения, представляющие практический интерес. Построена теория конических тел, обладающих максимальным запасом статической устойчивости при различных изопериметрических условиях. Получено экспериментальное подтверждение результатов теории, в том числе обнаруженного закона подобия, что позволяет рекомендовать найденные пространственные конфигурации в качестве формы устойчивого сверхзвукового летательного аппарата с малым сопротивлением и высокими несущими свойствами, обеспечивающими быстрое затухание колебаний тела около центра масс. Построена теория оптимальных пространственных тел минимального волнового сопротивления, вращающихся в гиперзвуковом потоке. Кроме исследований, связанных с выбором оптимальных форм аппаратов, летящих с большой скоростью, Сидняевым Н.И. выполнен цикл работ по сверхзвуковому обтеканию источников тепловыделения, а также развита линейная теория обтекания осесимметричных тел в условиях поверхностного массообмена, изучено обтекание затупленных тел в широком диапазоне скоростей набегающего потока.
С использованием аналитических и численных методов выявлены новые физические эффекты взаимодействия газа с источником тепломассообмена, сформулированы новые принципы формирования сверхзвуковых потоков с нужными для приложений свойствами, проведены расчеты влияния массоподвода на аэродинамические характеристики быстро летящих тел. Показана возможность эффективного управления параметрами теплообмена с помощью двухфазного вдува на обтекаемой поверхности. Предложен новый лагранжев метод расчета течений сред, описываемых уравнениями континуума без собственных напряжений. Метод основан на привлечении дополнительных уравнений для компонент якобиана перехода от эйлеровых к лагранжевым переменным, тем самым позволяя рассчитывать все параметры среды (включая плотность) из решения обыкновенных дифференциальных уравнений на фиксированных траекториях.
Исследования по механике вязких жидкостей развиваются Сидняевым Н.И., главным образом, по трем направлениям: пограничный слой, гидродинамическая неустойчивость и переход к турбулентности, развитие и приложение численных методов к решению уравнений Навье-Стокса, Эйлера, Прандтля. В течение многих лет эти исследования проводились в связи с запросами развития аэрокосмической техники, в частности, тепловой защиты летательных аппаратов. Основу многих исследований составили работы Н.И.Сидняева по гидродинамической устойчивости аэродинамических следов, вихревых слоев и течений в каналах. Что касается численных решений задач вязкой жидкости, то исследования в этом направлении всегда были связаны с идеей об особой эффективности прямых методов Галеркина в комбинации с конечноразностными процедурами. Один из таких подходов, известный как метод Галеркина-Петрова, оказался особенно полезным не только для решения линейных задач устойчивости, но и для анализа нелинейных колебательных и волновых процессов в течениях вязкой жидкости.
 Обширный цикл работ по гидродинамике вязких жидкостей на кафедре выполнен под руководством проф. Н.И.Сидняева. Продолжались традиционные для кафедры исследования фундаментальных свойств вязких потоков, дисперсных сред таких, как неустойчивость и переход к турбулентности, вихреобразование и перенос завихренности при обтекании тел конечных размеров, отрывы и автоколебания в зонах отрыва, образование и динамика поверхностей раздела и свободных поверхностей в вязких потоках, перестройки потока под воздействием внешних объемных и поверхностных сил. Выбор конкретных задач определялся актуальными запросами современной технологии, экологии, техники. Значительная часть проводимых исследований посвящена течениям со свободными поверхностями и с поверхностями раздела, в частности, капиллярным течениям в струях и пленках при различной геометрии удерживающих и формирующих поток твердых поверхностей.
Обширный цикл работ по гидродинамике вязких жидкостей на кафедре выполнен под руководством проф. Н.И.Сидняева. Продолжались традиционные для кафедры исследования фундаментальных свойств вязких потоков, дисперсных сред таких, как неустойчивость и переход к турбулентности, вихреобразование и перенос завихренности при обтекании тел конечных размеров, отрывы и автоколебания в зонах отрыва, образование и динамика поверхностей раздела и свободных поверхностей в вязких потоках, перестройки потока под воздействием внешних объемных и поверхностных сил. Выбор конкретных задач определялся актуальными запросами современной технологии, экологии, техники. Значительная часть проводимых исследований посвящена течениям со свободными поверхностями и с поверхностями раздела, в частности, капиллярным течениям в струях и пленках при различной геометрии удерживающих и формирующих поток твердых поверхностей.
Большой интерес представляют исследования Сидняева Н.И. по изучению свойств нелинейных, и особенно, сильно нелинейных волн в вязкой жидкости в условиях, когда они развиваются под воздействием сил давления в грунтах, силы тяжести и внешних воздействий. Исследование их с применением прямых методов приводит к нелинейным математическим моделям с диссипацией и дисперсией. Объект исследования составляют пограничные слои, ограниченные свободными поверхностями, и пограничные слои вблизи поверхностей раздела. Для адекватного описания движений свободной поверхности с большой амплитудой, например, сильно нелинейных волн, разработан способ соответствующего обобщения уравнений Прандтля. Выполнен большой цикл работ по аэрогидромеханике. Такие исследования включают: решение уравнений Навье-Стокса в приближении пограничного слоя для течений сред со свободными границами и границами раздела, исследование гидродинамической неустойчивости стационарных и нестационарных течений, анализ нелинейного развития возмущений и формирование волн.
Установлен ряд закономерностей фундаментального характера. Роль вязкости, формирующей профиль скорости в слое, оказывается существенной, т.к. может приводить к появлению профильной неустойчивости, отличной от неустойчивости Релея и Кельвина-Гельмгольца. Исследованы струйные течения, в которых развитием неустойчивости можно достаточно эффективно управлять с помощью наложенных вращений, геометрией удерживающей поверхности и свободной пленки. Новое развитие получила задача о пограничном слое на поверхности раздела, развивающемся под воздействием трения на поверхности. Проведенные расчеты спектров неустойчивости таких пограничных слоев открыли новые моды неустойчивости и наметили направление исследований для истолкования сложной картины турбулизации поверхности. Процессы гидродинамической неустойчивости, порождающие волновые структуры на поверхности, развиваются при сравнительно небольших числах Рейнольдса. Это обстоятельство позволяет успешно применять прямые методы для изучения динамики волновых пленок жидкости. Содержательная нелинейная модель течения построена осреднением по толщине пленки системы уравнений Навье-Стокса. Проведено численное исследование уравнений течений при задании в качестве начальных условий малых гармонических волн, а также регулярных нелинейных решений. Уравнения содержат внешний параметр, возрастающий вместе с числом Рейнольдса и средней толщиной пленки. Особое внимание уделено случаю малых волновых чисел, при которых на каждом пространственном периоде квазистационарной волны имеется четко выраженный участок невозмущенной поверхности, так что регулярная волна по существу представляет уединенную волну. Установлены общие закономерности динамики развивающихся волновых фронтов, которые заключаются в следующем. Все регулярные нелинейные волновые решения, также как малые гармонические волны, неустойчивы и автоматически перестраиваются в устойчивые волновые структуры.
В течение ряда лет на кафедре проводятся исследования по теории нелинейных волн в пленках. Решению модельных уравнений Сидняевым Н.И. посвящен целый ряд оригинальных работ и обзорных статей. Разработанные Сидняевым Н.И. методы находят эффективное приложение к изучению неустойчивости и нелинейных волн, усложненных процессами тепло- и массообмена. Анализ проблем обобщения и приложений модельных уравнений показал, что часто применяемые слабонелинейные модельные уравнения являются частными случаями модельных уравнений при стремлении к нулю единственного свободного параметра подобия, отражающего условия экспериментов. Как следствие этого, нелинейные волновые решения предельных модельных уравнений представляют лишь математические волны. Проведено подробное численное исследование нестационарных решений предельного модельного уравнения и построена наиболее полная картина динамики их развития во времени. В развитие проблемы о тепломассопереносе, выполнен ряд работ, в которых основной результат обобщен на другие случаи. В связи с нелинейностью основных уравнений численные методы играют существенную роль в аэрогидродинамике. Они применяются не только для доведения до конечного численного результата решений отдельных задач, но, главным образом, для выявления фундаментальных свойств течений. Особенно это относится к течениям вязкой жидкости. Развитие численных методов Сидняевым Н.И. ориентировано на применение прямых методов при гибком комбинировании их с методами конечных разностей. Численные методы решения линейных и нелинейных проблем гидродинамической устойчивости разрабатывались для изучения неустойчивости, нелинейного развития возмущений и переходов к сложным пространственным структурам в потоках с границами раздела и зонами отрыва, формирующихся в закрученных потоках и при обтекании плоских тел вязкой жидкостью. Исследованы критические значения параметров, при которых происходит потеря устойчивости стационарных течений, изучается нелинейный переход к новым периодическим или квазипериодическим состояниям и находятся решения уравнений Навье-Стокса для вторичных течений. В частности, решена проблема отыскания собственных чисел для системы уравнений Орра-Зоммерфельда в двух областях с условиями плавного сопряжения на границе раздела. Это создает возможность находить области неустойчивости и наиболее растущие возмущения в течениях. Численными экспериментами показано, что возможно надежное моделирование ламинарного и турбулентного закрученного течения с застойной зоной ламинарным потоком с эффективным числом Рейнольдса, которому соответствует подходящее решение уравнений Навье-Стокса. Для истолкования гидродинамических механизмов разрушения вихрей исследована неустойчивость закрученных потоков с застойной зоной, которые характеризуются тем, что основное течение не плоскопараллельное. Обнаружены новые моды для свободного вихря, изучено возникновение, исчезновение, переход мод друг в друга при изменении чисел Рейнольдса, закрутки, геометрических параметров.
Проведены исследования взаимодействий неустойчивостей и зон отрыва при обтекании профиля крыла с перфорированной и непроницаемой поверхностью дозвуковым и трансзвуковым потоком газа. Усовершенствована вычислительная схема для расчета базовой задачи об обтекании кругового цилиндра, сопровождаемым формированием нестационарной зоны отрыва с вихревой дорожкой, при учете перемещений цилиндра. Отработаны алгоритмы, программы и постановки задач, учитывающих развитие неустойчивости в пограничном слое от носика профиля до зон отрыва. Прямыми вычислениями показана возможность затягивания перехода и отрыва с помощью управляемого вдува. Включение перфорации поверхности в анализ позволяет конструировать сверхзвуковые течения, в которых зона отрыва, вызываемая размытым скачком, оказывается минимальной.
Новый нелинейный эффект обнаружен прямыми вычислениями в задаче о вторичных течениях после потери устойчивости вращающегося течения. Наряду с вихрями Тейлора, самопроизвольно развивающимися из малых возмущений, существуют также периодические структуры, которые устанавливаются при начальных возмущениях конечной амплитуды. Развиты математические модели пограничного слоя в условиях массопереноса. Широкий круг вопросов, связанных с теорией пластических деформаций, химической технологией, течениями многофазных сред, геофизикой и геологией, исследован профессором Н.И. Сидняевым, а также построена математическая модель фильтрации газа через тепловыделяющую грунтовую среду, на основе которой удалось объяснить данные наблюдений за поведением криолитозоны. Учет неньютоновских реологических свойств мантийных пород грунтов позволил воспроизвести ряд известных в геологии особенностей эволюции глобального геодинамического процесса в районах Крайнего Севера.



