Подробная история кафедры ФН1

Подробности
Категория: Общее
Страница 4 из 9

Научная работа

Круг научных интересов специалистов, работающих на кафедре, очень широк. По ряду направлений они занимают ведущие позиции в разрабатываемых проблемах теоретической и прикладной математики. Многие результаты, полученные преподавателями кафедры, получили признание не только в нашей стране, но и за рубежом. На кафедре работает научный семинар «Динамика возмущений в сплошных средах» под руководством профессоров А. Т. Ильичева и А. С. Савина, проводятся научные конференции по актуальным направлениям развития прикладной математики в энергетике, энергоэффективности и информационно-коммуникационных технологиях.

Основными направлениями исследований на кафедре являются:

  • Дифференциальные уравнения и уравнения в частных производных (проф. Филиновский А. В., доц. Гласко А. В., доц. Зорина И. Г., доц. Неклюдов А. В., доц. Станцо В. В., доц. Копаев А. В., доц. Павельева Е. Б., доц. Покровский Л. Д., доц. Аникин А. Ю.).
  • Теория вероятностей, математическая статистика, математическая теория надежности (проф. Белов В. Н., доц. Ветров Л. Г., проф. Калинкин А. В., проф. Павлов И. В., проф. Тимонин В. И., доц. Сунчалина А. Л.).
  • Исследование операций (проф. Васильев Н. С., проф. Грешилов А.А., проф. Смольяков Э.Р.).
  • Функциональный анализ и алгебра (проф. Исмагилов Р. С., доц. Табалдыев С. Б., доц. Храпов П. В., доц. Огнева О. С.).
  • Механика сплошной среды (проф. Ильичев А.Т., проф. Савин А. С., проф. Сидняев Н. И., доц. Томашпольский В. Я., доц. Федотов А.А., проф. Шахов Е. М., доц. Богомолов В. Г., доц. Бояринцева Т. Е., доц. Янов И. О.).
  • Теория атомарных и R – функций, вейвлеты, фракталы (проф. Кравченко В. Ф., ст. преп. Коновалов Я.Ю.).

 

Фундаментальные научные направления

1. Дифференциальные уравнения и уравнения в частных производных.

Профессор Филиновский Алексей Владиславович, доктор физико-математических наук, крупный специалист в области уравнений математической физики. Он автор более 100 научных работ, им опубликованы 2 монографии по исследуемой тематике. Его научные результаты относятся к решению задач стабилизации при больших значениях времени решений нестационарных смешанных задач для эллиптических операторов в неограниченных областях; исследованию экстремальных задач для уравнений в частных производных; изучению спектральных свойств несамосопряженных краевых задач. Среди главных результатов:

  • изучено асимптотическое поведение при больших значениях времени решений внешних краевых задач для нестационарных уравнений высокого порядка;
  • получены интегральные оценки скорости убывания решений первой смешанной задачи для волнового уравнения в областях с компактными незвездными границами;
  • получены равномерные по спектральному параметру оценки резольвентны первой краевой задачи для оператора Лапласа и ее производной по спектральному параметру в неограниченных областях;
  • получено достаточное условие непрерывности спектра первой краевой задачи для полигармонического оператора в областях с некомпактными границами;
  • изучены классы существования решений экстремальных задач с несамосопряженными краевыми условиями для параболических уравнений.

Результаты исследований частично изложены в монографиях:

  • Асташова И.В., Кондратьев В.А., Муравей Л.А., Филиновский А.В. Качественная теория дифференциальных уравнений. – М.: МАТИ-РГАТУ, 2001. – 141с.
  • Astashova I.V., Filinovskii A.V., Kondratiev V.A., Muravey L.A. Some Problems in Qualitative Theory of Differential Equations. – London.; Jnan Bhawan Publishers, 2002.

Доцент Гласко Андрей Владленович, кандидат физико– математических наук, автор около 30 научных работ.
Область научных интересов Гласко А.В. распространяется на использование уравнений математической физики для создания математических моделей, моделирующих как поведение живых систем, так и процессы самоорганизации искусственных систем (в частности, наноматериалы).
К основным результатам относятся:
- создана и частично обоснована математическая модель динамики внимания в процессе восприятия элементарного внешнего стимула;
- разработка модели конвергентных процессов, имеющей приложения в процессе описания самоорганизации материи и самосборки наноструктур, представляющих основу восходящих технологий.
Доцент Павельева Елена Борисовна, кандидат физико – математических наук, автор около 10 научных работ. Занимается исследованием асимптотических свойств решений уравнения переноса излучения в неодномерных протяженных цилиндрических областях.
На основе асимптотической теории разработаны алгоритмы поиска асимптотических режимов в протяженных неодномерных цилиндрических областях и получены тестовые результаты для радиационных полей в задачах о глубоко проникающем излучении.

Доцент Неклюдов Алексей Владимирович, кандидат физико – математических наук. Область научных интересов – изучение поведения решений эллиптических уравнений, в т.ч. нелинейных, в неограниченных областях. Получены результаты по поведению решений задачи Неймана для уравнений произвольного порядка в областях, близких к цилиндрическим. Исследованы особенности решений в цилиндрической области нелинейного уравнения второго порядка с экспоненциальной нелинейностью. Результаты исследований опубликованы в нескольких статьях журналов АН Российской Федерации.

Доцент Станцо Виталий Владимирович, кандидат физико–математических наук. Он является специалистом по качественной теории дифференциальных уравнений. Его исследования посвящены исследованию возникновения предельных циклов в трехпараметрических двумерных динамических системах. В частности, ему принадлежит результат, показывающий, что количество таких циклов в ограниченной области может быть сколь угодно большим. Интенсивно занимается вопросами приложений дифференциальных уравнений в экономико-математическом моделировании. Станцо В.В. опубликовал 20 научных работ по теоретическим и прикладным вопросам теории дифференциальных уравнений.
Доцент Зорина Ирина Григорьевна, кандидат физико – математических наук. Имеет более 10 научных публикаций по исследованию процессов теплообмена при фазовопереходных процессах в различных средах. Получены интересные результаты в теории подобия систем плазменной аэродинамики. Ее работы нашли практическое применение, в частности, при оптимизации ультразвуковых составных электроакустических преобразователей для обработки инфицированных ран.

Доцент Покровский Леонид Дмитриевич, кандидат физико – математических наук. Высококвалифицированный специалист по задачам газовой динамики с нелинейной теплопроводностью, теории пограничного слоя. Его главные результаты относятся к области классификации и свойств решений уравнения переноса с нелинейностями общего вида (включая турбулентную фильтрацию).
Леонид Дмитриевич в совершенстве владеет французским языком, что позволяет ему регулярно принимать участие в научных конференциях во Франции. Автор около 40 научных и методических работ. Он подготовил 3 кандидата физико – математических наук (среди них доцент кафедры Гласко А. В.).

Доцент Копаев Анатолий Владимирович – кандидат физико – математических наук. Его научные интересы сосредоточены в области решения краевых задач теории аналитических функций (одной и нескольких переменных) и их применения в математической физике. Им предложен универсальный метод «функциональных уравнений» для решения задач сопряжения аналитических и гармонических функций, возникающих при описании установившихся фильтрационных течений несжимаемой жидкости в кусочно-однородных средах. Для решения одного из важнейших функциональных уравнений удалось построить интегро-дифференциальное преобразование, которое каждой гармонической в полупространстве функции трех переменных ставит в соответствие гармоническую в полуплоскости функцию двух переменных, зависящую от одного действительного параметра, а также найдено обратное преобразование. А.В. Копаевым опубликовано более 20 работ по данной тематике.

Доцент Аникин Анатолий Юрьевич, кандидат физико – математических наук, ведет исследования в области динамических систем классической механики. Основные направления его работы: гамильтонова динамика; хаос и интегрируемость в гамильтоновой динамике; локальные методы в гамильтоновой динамике; квазиклассический анализ; квантовая и статистическая механика с точки зрения классической. Им опубликованы три работы в зарубежных изданиях, в которых, в частности, доказан квантовый аналог теоремы Мозера о сходимости нормализующего преобразования для случая полутора степеней свободы; получен альтернативный язык, более алгебраический по сравнению со стандартным, для канонического формализма в неавтономном случае; получен квантовый аналог этого языка.

 

2. Теория вероятностей, математическая статистика, математическая теория надежности.
На кафедре сложился сильный коллектив специалистов, работающих в области теории вероятности и математической статистики, а также научных и технических приложений этих направлений. В частности, в области планирования, проведения и анализа результатов ускоренных испытаний, оценки надежности изделий в переменных режимах, а также прогнозирования показателей надежности сложных систем кафедра является одним из основных центров разработки новых идей и направлений.

Профессор Белов Владимир Николаевич, доктор технических наук, автор 60 научных работ и 2 монографий. Является известным специалистом в области оценки показателей надежности сложных технических систем. Основное направление исследований: моделирование (скалярное, векторное) временных процессов различной природы.
Полученные результаты:

  • построены функционалы специального вида, позволяющие (при достаточно общих ограничениях на временной процесс) осуществлять пересчеты характеристик процесса от одних условий реализации к другим (статический, циклический, динамический режимы). Это позволило построить методы прогнозирования характеристик временного процесса в условиях (статических, циклических), требующих проведения длительных экспериментов, по результатам кратковременных испытаний (например, в динамических режимах);
  • разработана процедура построения режима изменения внешних условий, обеспечивающего изменение требуемой характеристики процесса по заданной (но реализуемой) траектории;
  • разработаны методы прогнозирования показателей надежности изделий радиоэлектроники в условиях эксплуатации по результатам лабораторных испытаний.

Частично результаты исследований представлены в двух монографиях:

  • Белов В.Н. Детерминированные модели временных процессов. – Волгоград: Политехник, 2002;
  • Белов В.Н. Стохастические модели временных процессов. – Волгоград: Политехник, 2002.

Доцент Ветров Леонид Георгиевич, кандидат физико – математических наук. Являясь специалистом по теории вероятности (основные работы относятся к теории фильтрации мартингалов), он получил ряд интересных результатов в самых разнообразных прикладных областях. Им, в частности, исследовались вопросы построения системы бонус – малус в задачах автострахования; разработаны модели и методы проведения форсированных испытаний сложных систем и систем «без памяти»; получены модели поведения игроков на финансовом рынке валютных «фьючерсов». По этим направлениям им опубликовано более 40 научных публикаций в нашей стране и за рубежом.

Профессор Калинкин Александр Владимирович, доктор физико-математических наук. Опубликовал около 60 научных работ по исследованию и моделированию стохастических систем с взаимодействием с марковскими процессами при дискретных состояниях.
Разработанные им схемы взаимодействия широко используются для исследования вероятностных объектов физической кинетики, химической кинетики, экологии, в теории надежности технических систем (на рис. 2 представлены фазовая плоскость (а) и гистограмма (б)). Основные результаты:

  • введены и классифицированы общие марковский процессы со взаимодействием при счетном множестве состояний на основе схемы взаимодействий;
  • разработаны новые методы решения уравнений Колмогорова для производящих функций переходных вероятностей в нестационарном и стационарном случаях;
  • для ряда процессов со взаимодействием выявлено нелинейное свойство (кинетическое уравнение) переходных вероятностей путем построения точных замкнутых решений первого и второго (линейных) уравнений Колмогорова.

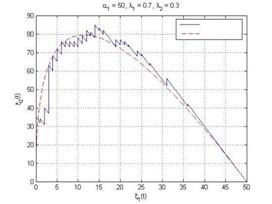
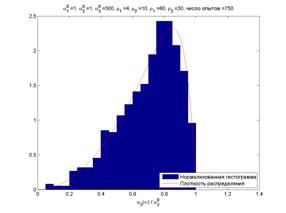
Полученные результаты: найдены решения первого и второго (линейных) уравнений Колмогорова для специальных классов марковских процессов: ветвящихся процессов, ветвящихся процессов с взаимодействием и других. Марковские процессы с взаимодействием определяются как модели эволюции систем частиц нескольких типов, согласно данной кинетической схеме. В случае независимости эволюций отдельных частиц друг от друга известно обыкновенное нелинейное дифференциальное уравнение для одночастичной производящей функции переходных вероятностей (кинетическое уравнение для одночастичной функции распределения). Фундаментальная проблема вывода третьего (нелинейного) уравнения теории марковских процессов разрешима через построение точных замкнутых решений линейных уравнений Колмогорова. Результаты исследований частично изложены в монографии “Markov’s branching processes with interaction”, Russian Mathematical Surveys, 2002, v. 57, p. 241-304.

Профессор Павлов Игорь Валерианович, доктор физико-математических наук. Лауреат премии правительства РФ в области науки и техники за 2003 г. Видный специалист в области оценки и прогноза надежности больших технических систем на основе данных по испытаниям их компонент (элементов, подсистем). Его научные результаты отражены более чем в 60 научных трудах, а также в двух монографиях. Одним из основных направлений научной работы кафедры высшей математики (ФН -1) является математическая теория надежности и ряд связанных с ней направлений:

  • Надежность и безопасность сложных технических систем, таких как современные системы энергетики, транспортные сети, системы радиоэлектроники, приборостроения и др.
  • Испытания сложных технических систем
  • Ускоренные испытания
  • Оценка остаточного ресурса сложных технических систем

Математическая теория надежности как система соответствующих идей, математических моделей и методов оценки, прогноза и оптимизации показателей надежности, начала развиваться в послевоенные годы в связи с возрастающими требованиями к новой сложной технике. В 50-х годах вопросы надежности, испытания на надежность и задачи повышения надежности ракет и электронного оборудования стали привлекать значительное внимание, как математиков, так и инженеров – разработчиков новой техники. После чего в последующие годы появилось значительное число работ в этой области, в основном российских и американских ученых. При этом многие исследования шли параллельно и в некоторых вопросах удалось продвинуться дальше американским специалистам, а в некоторых – нашим. Основные работы сотрудников кафедры высшей математики МГТУ им. Н.Э.Баумана в области математической теории надежности и смежных областях.
Научные результаты:

  • разработан метод определения наименьшего доверительного множества для вероятности безотказной работы сложной системы по аналогичным характеристикам ее компонент;
  • получены оптимальные стратегии управления процессами замен и восстановления оборудования в сложных информационно – вычислительных комплексах;
  • решена задача оптимального распределения вычислительных мощностей в системах с параллельными вычислительными модулями;
  • исследованы оптимальные методы последовательной проверки сложных гипотез и доверительного оценивания функций многих неизвестных параметров.

Основные научные результаты отражены в монографиях:

  • Павлов И.В. Статистические методы оценки надежности сложных систем. М.:Радиосвязь, 1982.;
  • Гнеденко Б.В., Павлов И.В., Ушаков И.А. Статистическая теория надежности. Нью – Йорк, Wiley, 1999 г. (на англ. языке).

Профессор Тимонин Владимир Иванович, доктор физико-математических наук, является автором около 40 научных работ в области непараметрической статистики, методов анализа результатов научных и технических экспериментов, а также применений этих методов в теории надежности, автострахования и медицины.
Основные научные результаты Тимонина В.И. относятся к области исследования распределений классических статистик типа Колмогорова – Смирнова в двух – и многовыборочных вариантах, а также для полных и цензурированных выборок (статистики Реньи). К наиболее значительным результатам относятся:

  • получен общий метод вычисления точных распределений любых статистик типа Колмогорова – Смирнова при справедливости степенных связей Кокса – Лемана между функциями распределения нескольких независимых выборок;
  • впервые рассмотрена задача проверки степенных гипотез Кокса – Лемана в качестве основных и предложен критерий их проверки;
  • для прогрессивно цензурированных выборок исследован критерий проверки их однородности и получены точные и асимптотические распределения его статистики, использующей оценки Каплана – Мейера функции выживания.

Доцент Сунчалина Анна Леонидовна, кандидат физико – математических наук, ведет исследования в области оптимизации проведения форсированных испытаний. За счет использования параметрических двумерных моделей наработок до отказа изделий в разных режимах, основанных на ортогональном разложении плотностей, ей удалось существенно повысить точность определения корреляционных связей между этими наработками. Кроме того, ею существенно обобщены результаты Г.Д. Карташова в моделях форсированных испытаний сложных систем. Сунчалиной А. Л. опубликовано около 10 научных работ по этим направлениям.

 

 

3. Исследование операций

Работы в данном направлении ведутся как в теоретическом, так и прикладном направлениях.

Профессор Васильев Николай Семенович, доктор физико-математических наук, крупный специалист в области оптимального управления и численных методов, автор более 40 научных работ. Его основные результаты охватывают широкий спектр проблем:

- получены теоремы существования в минимаксных задачах и в дифференциальных играх;

- предложены методы поиска глобального экстремума  в вогнутых задачах и поиска равновесий в n-матричных играх;

- исследованы модели глобальных сетей, для которых построены алгоритмы оптимальной маршрутизации сообщений на основе многокритериального подхода.

На основе полученных результатов предложены новые (многокритериальные и игровые) модели маршрутизации глобальных пакетных сетей, в которых осуществляется оптимизация быстродействия в условиях неопределенности и изменяющейся входной нагрузки. Разработан эффективный распределенный алгоритм управления маршрутами передачи, допускающий применение в режиме реального времени и обеспечивающий устойчивость потоков в сети. Проведенная серия вычислительных экспериментов с моделями глобальной сети Интернет, в частности с ее европейской частью, показала, что на этом пути может быть решена проблема эффективного обмена данными.

Профессор Грешилов А.А. – доктор технических наук, автор более 150 научных статей, 20 изобретений, 13 монографий. Он является одним из крупнейших российских специалистов по разработке и применению математических методов в анализе результатов научных экспериментов, имеющих важнейшее значение для страны. Основные направления его деятельности – ядерная физика (физика деления ядер), конфлюэнтный анализ, некорректные задачи, математические методы принятия решений.

Грешилов А.А. разработал оригинальные методы определения параметров ядерных взрывов по газообразным продуктам деления, а также параметров их нейтронного и гамма – излучений. Под его руководством создана подсистема перспективного планирования соответствующей отрасли. Математические модели конфлюэнтного анализа и методы оценки их параметров, автором которых является Грешилов А.А., стали теоретической основой разработки ряда спецпроектов.

Важное значение имеют разработанные им  новые методы решения некорректных задач в многосигнальной радиопеленгации на одной частоте, позволяющие значительно повысить точность работы радиолокаторов. По этому направлению получено несколько авторских свидетельств.

Книги и монографии Грешилова А.А. как нельзя лучше отражают широчайший кругозор и глубину проработок решаемых им задач:

  • Грешилов А.А. Некорректные задачи цифровой обработки информации и сигналов.- М.: Радио и связь, 1984.;
  • Грешилов А.А. Прикладные задачи математического программирования. М.: Логос, 2006.;
  • Ракетно-ядерное оружие и системы противоракетной обороны. Меч и щит России./ Коллектив авторов./ Калуга. Информационное агентство «Калуга-пресс», 2007.;
  • Грешилов А.А., Егупов Н.Д., Матущенко А.М. Ядерный щит. – М.: Логос, 2008.

Профессор Смольяков Эдуард Римович – доктор физико – математических наук, автор около 200 научных работ, среди которых около 10 монографий. Смольяков Э.Р. является выдающимся специалистом в области теории игр и теории управления.

Смольяковым Э.Р. создана теория конфликтов, которую можно рассматривать как радикально новую теорию любых статистических и динамических игр. Эта теория предоставляет возможность получать решение, причем почти всегда единственное, любых конфликтных задач и игр – антагонистических, некооперативных, кооперативных и иных типов, как статических, так и динамических. Существенно, что эта теория дает единообразный подход к решению любых типов конфликтных задач, в отличие от классической теории игр, в которой задачи разных типов изучались независимо друг от друга и для которых не удавалось зачастую находить хотя бы какое – то решение.

На основе этой теории Смольяков Э.Р. построил математическую теорию быстрых межгалактических перелетов по каналам в магнитной вселенной, двойственной к нашей вселенной, а также разработать новое направление исследований, пограничное между математикой и физикой – экстремальную теорию размерностей, позволившую выводить точные дифференциальные уравнения любых процессов без использования физических законов и находить новые физические закономерности чисто математическим путем.

Во многом необычные и неожиданные результаты Смольякова Э.Р. изложены в ряде книг, в том числе:

  • Смольяков Э.Р. Неизвестные страницы истории оптимального управления. М.:Едиториал УРСС, 2002;
  • Смольяков Э.Р. Теория конфликтных равновесий. М.:Едиториал УРСС, 2005;
  • Смольяков Э.Р. Теоретическое обоснование межзвездных перелетов. М.:КомКнига, 2005.

 

4. Функциональный анализ и алгебра

Профессор Исмагилов Раис Сальманович, доктор физико-математических наук. Один из блестящих математиков – теоретиков, имеющих глубокие результаты в самых абстрактных областях функционального анализа и алгебры. Опубликовано более 60 работ в изданиях, имеющих высший рейтинг как в России, так и за рубежом. Главные из результатов:

Спектральная теория операторов.

- изучены спектральные свойства классических операторов; получены результаты о спектре операторов Штурма-Лиувилля;

- построен аналог формулы Фейнмана-Каца для локально-компактных  несвязных полей.

2. Представления групп.

- построены представления групп отображений многообразий в группы Ли, которые впоследствии были названы энергетическими;

- построены представления ряда классов бесконечномерных групп.

3. Теория приближений.

- решена одна из старейших классических задач о колмогоровских поперечниках функциональных классов; предложен метод усреднения в исследовании этих величин, оказавшийся весьма сильным средством исследования.

Результаты по теории представления групп опубликованы в монографии «Representations of infinite dimensional groups», AMS, v. 152.

Доцент Табалдыев Сейтек Болотбекович, кандидат физико – математических наук, – работает в области топологической гомологии – области функционального анализа, изучающей банаховы и локально выпуклые топологические алгебры  и их непрерывные представления (банаховы и топологические модули) с использованием методов гомологической алгебры.

Главные научные результаты связаны с исследованием связи неприводимости, пространственной проективности операторной алгебры, нетривиальности её коммутанта и возможнвм наличием в этой алгебре столбца одномерных операторов. Табалдыевым С.Б. доказана неинъективность предуального бимодуля для алгебр мер на бесконечных дискретных группах. Учитывая, что алгебра мер на аменабельной группе аменабельна по Конну, тем самым отрицательно решён известный вопрос об инъективности предуального бимодуля для таких алгебр.

Результаты Табалдыева С.Б. опубликованы в 5 работах в ведущих российских и зарубежных журналах.

Доцент Храпов Павел Васильевич, кандидат физико – математических наук. Высококвалифицированный специалист в области функционального анализа, численных методов, методов оптимизации. Имеет более 30 научных публикаций. С 1986 является председателем студенческого научно-технического общества кафедры «Высшая математика» и председателем оргкомитета ежегодной студенческой научно-технической конференции кафедры «Весна». С 1988 член Московского Математического общества.

Основным направлением исследований  является теория перколяции, модель Изинга в математической физике. Много занимался и прикладными вопросами статистического анализа – исследованию валютного рынка FOREX, разработкой методов анализа Data Mining (кластеризация, классификаторы, прогнозирование).

Доцент Огнева Ольга Семеновна, кандидат физико – математических наук. Основными направлениями ее исследований являются гомология топологических алгебр и анализ стохастических систем. Ее результаты нашли отражение в 10 научных работах, опубликованных в центральных изданиях.

 

5. Механика сплошной среды.

По этой тематике на кафедре работает ряд крупных специалистов, возглавляющие соответствующие направления в учреждениях АН РФ (МИ АН им. Стеклова, ВЦ АН РФ им. Дородницына и др.).

 

Профессор Ильичев Андрей Теймуразович, доктор физико-математических наук.

Его научные интересы сосредоточены в области теории распространения волн в диспергирующих средах, устойчивости локализованных волновых структур, исследовании поверхностей раздела в задачах гидромеханики, теории упругости и теории фильтрации. Он является автором свыше 30 научных работ. Главные результаты его работ приведены в монографии

Ильичев, А. Т. Уединенные волны в моделях  гидромеханики. – М.: Физматлит, 2003. Профессор Ильичев А.Т. активно участвует в подготовке квалифицированных кадров преподавателей для кафедры. Его ученик, доцент кафедры Томашпольский В.Я., защитил диссертацию по тематике Андрея Теймуразовича, касающуюся распространения волн в упругих средах.

Профессор Савин Александр Сергеевич, доктор физико-математических наук. Автор более 50 работ в задачах взаимодействия неоднородностей с границами раздела жидкостей с различными плотностями.

Неоднородности различной природы, например, обтекаемые потоком преграды, источники массы, вихревые структуры и т.д., вызывают возмущения границ раздела сред. Расчет таких возмущений составляет содержание прямой задачи. В последнее время разработка систем мониторинга окружающей среды привела к необходимости восстановления физических полей в толще морской среды по данным зондирования границ раздела слоев с различными плотностями, в частности – свободной поверхности. При этом возникла гидродинамическая проблема: получить сведения о внутренней структуре потока по данным о его границах. Существенной частью этой общей проблемы является обратная задача генерации поверхностных и внутренних волн погруженными в поток неоднородностями.

Научные результаты:

  • обобщен метод М.В.Келдыша на случай произвольного закона движения гидродинамических особенностей переменных интенсивностей;
  • исследован характер установления поверхностных волн, генерируемых гидродинамическими особенностями;
  • описано самоиндуцированное движение точечного вихря под свободной поверхностью жидкости;
  • предложены различные подходы к задаче продолжения гидродинамических полей в толщу потока с его границы.

Результаты исследований частично изложены в монографии Савин А.С. Методы, процедуры и средства аэрокосмической компьютерной радиотомографии приповерхностных областей Земли. – М.: Научный мир, 1996.

Профессор Шахов Евгений Михайлович, доктор физико-математических наук. Один из наиболее известных специалистов в области механики жидкости и газа. Основные и наиболее важные результаты получены в кинетической теории газов. По этой тематике им опубликовано около 120 работ. К главным результатам относятся:

  • - разработка метода аппроксимации канонического уравнения Больцмана;
  • - новая кинетическая модель, или модель Шахова;
  • - обобщение существующих численных конечно-разностных методов решения кинетических уравнений и решение на этой основе  широкого спектра задач;
  • - разработка способа определения локальных значений плотности и градиента плотности разреженной планетарной атмосферы по колебаниям легкого спутника-зонда, буксируемого орбитальным летательным аппаратом;
  • - исследование основных закономерностей развития пространственных вихревых движений вязкой несжимаемой жидкости в полости тела, ускоренно вращающегося вокруг оси симметрии и/или около неподвижной точки (гироскопы с жидким наполнением).

 

Доцент Федотов Анатолий Александрович, кандидат физико – математических наук, автор около 30 научных работ.

Основные научные интересы: уравнения математической физики в механике сплошной среды, численные методы.

Главные научные результаты связаны с математическим моделированием работы машущего крыла в природе и технике:

- разработка математической модели крыла, работающего в режиме нормального трепещущего полета;

- разработка математической модели хвостового плавника дельфина, объясняющей происхождение оптимального способа плавания дельфина.

Федотов Анатолий Александрович – один из авторов патента РФ «Объемное голографическое антенное устройство».

Доцент Бояринцева Татьяна Евгеньевна, кандидат физико – математических наук, автор более 10 научных работ. Ее исследования посвящены вопросам обнаружения различных вихревых структур в идеальной жидкости. Методы, развиваемые в ее работах, тесно связаны с задачами аэрокосмической компьютерной радиотомографии приповерхностных областей Земли. Руководит издательской деятельностью кафедры.

 

Доцент Богомолов Владимир Георгиевич, кандидат физико – математических наук. Его работы посвящены вопросам взаимодействия оболочечных конструкций с жидкостью и динамике упругой оболочки в жидкости. Им опубликовано около 20 научных работ. Руководит методическим семинаром кафедры.

 

Доцент Янов Игорь Олегович, кандидат технических наук. Специализируется в области исследования динамики систем ориентации самолетов и космических аппаратов с использованием солнечного давления, а также идентификации параметров водопроводных сетей. В течение долгого времени работал по совместительству на кафедре ИУ-3 в должности старшего научного сотрудника. Является автором около 50 научных работ и 3 изобретений.

 

 

6. Теория атомарных и R – функций, вейвлеты, фракталы.

На кафедре работает один из создателей данного направления в современной математике.

 

Профессор Кравченко Виктор Филиппович – заслуженный деятель науки РФ, доктор физико – математических наук, профессор, Главный научный сотрудник Института радиотехники и электроники РАН, главный редактор и основатель международного журнала «Электромагнитные волны и электронные системы», а также «Успехи современной радиоэлектроники», автор более 650 научных работ, в числе которых 20 монографий и 11 авторских свидетельств. В.Ф. Кравченко – основатель научной школы: под его руководством защищено 10 докторских и 17 кандидатских диссертаций. Один из ведущих в мире специалистов в новейших областях современной математики – теории атомарных и R – функций, вейвлетов, фракталов. Его научные достижения находят широкое применение на практике: в цифровой обработке сигналов и изображений, в краевых задачах математической физики. Он участвовал в многочисленных международных симпозиумах и конференциях.

Основные научные результаты следующие:

  • решены на основе теории R – функций для областей сложной формы краевые задачи электродинамики, теплопроводности, акустики; исследованы проблемы, связанные с построением координатных последовательностей для основных вариационных и проекционных методов, краевых условий различных типов и областей сложной формы;
  • решены с помощью нового типа эквивалентных граничных условий (задачи третьего рода) внутренние и внешние краевые задачи электродинамики сверхпроводящих структур:
  • разработана теория сверхпроводящих резонаторов, позволившая получить эффективные алгоритмы по уточнению фундаментальной физической константы скорости света;
  • разработана на основе атомарных функций (АФ) теория цифровой обработки сигналов;
  • созданы новые классы весовых функций и новый класс WA – систем функций Кравченко – Рвачева;
  • на основе АФ исследованы обобщенные ряды Котельникова и полиномы Левитана;
  • решены задачи анализа и синтеза антенн на основе АФ;
  • разработан новый класс атомарно-фрактальных функций и создана теория фрактальных антенных решеток;
  • исследованы физические модели электродинамических и тепловых полей, позволившие решить задачи радиолокационного и радиотеплового картографирования подстилающих поверхностей различной природы с помощью космических аппаратов.

Кравченко В.Ф. – главный редактор журналов «Электромагнитные волны и электронные системы», «Успехи современной радиоэлектроники».

Основные научные издания Кравченко В.Ф.за последние годы:

  • В.Ф. Кравченко Лекции по теории атомарных функций и некоторым их приложениям. М.: Радиотехника, 2003.
  • В.Ф. Кравченко, В.Л. Рвачев Алгебра логики, атомарные функции и вейвлеты в физических приложениях. М. Физматлит, 2006.
  • В.К. Волосюк, В.Ф. Кравченко Статистическая теория радиотехнических систем дистанционного зондирования и радиолокации. Под ред. В.Ф. Кравченко М.: Физматлит, 2008.
  • В.А. Дорошенко, В.Ф. Кравченко. Дифракция электромагнитных волн на незамкнутых поверхностях. Под ред. В.Ф. Кравченко. М.: Физматлит, 2009.
  • В.Ф. Кравченко, О.С. Лабунько, А.М. Лерер, Г.П. Синявский. Вычислительные методы в современной радиофизике. Под ред. В.Ф. Кравченко. М.: Физматлит, 2009.