История кафедры ФН-1
«Математика – наука о количественных отношениях и
пространственных формах действительного мира»
Кафедре «Высшая математика» Московского государственного технического университета им. Н.Э. Баумана свыше – 140 лет.
Именно возраст заставил нас обратиться к истории кафедры, коллектив которого вписал не одну замечательную страницу в становление славы нашего университета.
Профессорско-преподавательский коллектив кафедры принимал самое активное участие в формировании базового образования, глубокой общенаучной и общеинженерной подготовки специалиста широкого профиля, способного работать не только по своей узкой специальности, но и в смежных областях науки и техники. И мы гордимся тем, что в достижения выпускников нашего вуза вложен и наш труд. Труд педагогического коллектива, усилиями которого успешно решается главная задача университета — обеспечение студентов современными знаниями в области математики. За время своего существования наш вуз выпустил, по самым скромным подсчетам, более 150 тысяч инженеров. И в успехах каждого из них есть вклад преподавателей кафедр, составляющих факультет «Фундаментальные науки» сегодня.
За время существования кафедры сменилось не одно поколение педагогов. Мы помним наших учителей – ученых и педагогов, усилиями которых была сформирована педагогическая школа воспитания инженеров, названная «русской». Конечно, упомянуть всех их в этом издании не представляется возможным, но мы испытываем чувство огромной благодарности ко всем, кто своим самоотверженным трудом ученого, педагога, воспитателя выковал целую плеяду инженерных кадров нашей Родины.
Предлагаемое вниманию читателя издание представляет собой коллективный труд. В подготовке материалов для него, уточнении содержания и редактировании участвовали несколько человек. Активное участие принимали в сборе материалов и сотрудники музея МГТУ им. Н.Э. Баумана.
Мы надеемся, что данное издание станет еще одним свидетельством славных традиций МГТУ им. Н.Э. Баумана, воспитанных многими поколениями ученых, педагогов, выпускников.
История развития математического образования на кафедре «Высшая математика»
 Становление научной школы математики в МГТУ им. Н.Э. Баумана связано с именем Алексея Васильевича Летникова (1837-1888), возглавившего в 1868 г. кафедру высшей математики и аналитической механики, созданную при преобразовании Московского ремесленного учебного заведения в Императорское Московское техническое училище. В 1878 г. из состава этой кафедры выделилась кафедра высшей математики, которой А.В.Летников продолжал руководить до конца своей жизни.
Становление научной школы математики в МГТУ им. Н.Э. Баумана связано с именем Алексея Васильевича Летникова (1837-1888), возглавившего в 1868 г. кафедру высшей математики и аналитической механики, созданную при преобразовании Московского ремесленного учебного заведения в Императорское Московское техническое училище. В 1878 г. из состава этой кафедры выделилась кафедра высшей математики, которой А.В.Летников продолжал руководить до конца своей жизни.
А.В.Летников родился в Москве, окончил здесь гимназию и Межевой институт, был в течение двух лет вольнослушателем Московского университета, а затем три года слушал лекции крупных французских математиков Серре, Шаля, Бертрана, Лиувилля, Пьюизе и других в парижской Политехнической школе при Сорбонне. В 1860 г. он вернулся в Москву и начал читать курс теории вероятностей в Межевом институте.
В первом томе «Математического сборника» (1866) А.В.Летников опубликовал свою первую научную работу по теории дифференциальных уравнений, в том числе уравнения Риккати. В 1867 г. ему была присуждена степень доктора Лейпцигского университета по теории дифференциальных уравнений. Международное признание дало ему право без университетского диплома сдать магистерские экзамены, а затем и успешно защитить магистерскую диссертацию на тему «Теория дифференцирования с произвольным указателем».
Идеи магистерской диссертации А.В. Летникова «Теория дифференцирования с произвольным указателем» были в дальнейшем развиты им в докторской диссертации «Исследования, относящиеся к теории интегралов вида
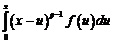
напечатанной в «Математическом сборнике» (т. 7, 1874 г.). При помощи предложенной им теории дифференцирования с дробным показателем ему удалось создать новый метод анализа особенностей решений обыкновенного дифференциального уравнения
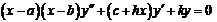
которое обобщает важные классы дифференциальных уравнений: гипергеометрическое, Бесселя, уравнения многочленов Лежандра и Чебышева. В 1882-1885 гг. в тт. 10-12 «Математического сборника» он опубликовал статьи о модификации этого метода применительно к сферическим функциям. Научные труды А.В.Летникова заслужили всеобщее признание, что было подтверждено избранием его членом-корреспондентом Петербургской академии наук.
Идеи А.В.Летникова в работах этого цикла непосредственно перекликались с идеями магистерской диссертации М.Е.Ващенко-Захарченко «Символическое исчисление и приложение его к интегрированию линейных дифференциальных уравнений» (1862 г., Киев) об упрощении решения дифференциальных и разностных уравнений. Серия работ английского ученого О.Хевисайда по применению операционного исчисления к решению электротехнических задач была начата лишь в 1887 г., причем в этих работах использовались подходы, сходные с идеями М.Е.Ващенко-Захарченко и А.В.Летникова, но без достаточно строгого математического обоснования. Научная работа А.В.Летникова была тесно связана с его педагогической деятельностью, что сыграло важную роль в математической подготовке инженеров в училище. Сложился характерный для А.В.Летникова стиль чтения лекций: простота, ясность при одновременной оригинальности математических доказательств.
Программа курса математики для различных отделений училища в то время включала аналитическую геометрию, анализ, сферическую геометрию, начала дифференциальной геометрии и высшей алгебры. Из специальных курсов выделялся прочитанный А.В.Летниковым курс вариационного исчисления, позднее вышедший отдельным изданием. Он был автором руководств по общим разделам анализа — дифференциальному и интегральному исчислению и их приложениям, дифференциальным уравнениям.
А.В.Летников помимо кафедры высшей математики возглавлял в училище и комиссию по разработке общей системы теоретической и практической подготовки инженеров, получившей всемирную известность как «русский метод обучения ремеслам», преподавал математику в Межевом институте, а с 1883 г. был директором Московского коммерческого училища. Будучи одним из инициаторов создания и учредителей Московского математического общества, ученый сделал на его заседаниях 15 докладов, материалы которых печатались в выпускаемом этим обществом «Математическом сборнике». В частности, в т. 3 этого сборника (1868) он впервые опубликовал на русском языке в своем переводе с немецкого одну из определяющих работ Н.И.Лобачевского «Геометрические основания теории параллельных». В предисловии к этой публикации А.В.Летников по достоинству оценил революционный переворот в геометрии, осуществленный Н.И.Лобачевским, и в дальнейшем в числе немногих русских математиков настойчиво пропагандировал его идеи. По инициативе А.В.Летникова в «Математическом сборнике» был создан специальный раздел по вопросам методики преподавания математики, причем не только высшей, но и элементарной. В этом разделе он напечатал несколько статей методического характера. Этим же вопросам была посвящена его речь «О системах реального образования», произнесенная им в ИМТУ в 1871 г. во время ежегодной торжественной церемонии выпуска студентов.
 С 1872 г. начал свою работу в училище в должности преподавателя математики выдающийся русский ученый-механик, создатель кафедры теоретической механики в ИМТУ Николай Егорович Жуковский (1847-1921), который своими математическими исследованиями оказал влияние на развитие научной школы математики, в том числе в области качественной теории дифференциальных уравнений.
С 1872 г. начал свою работу в училище в должности преподавателя математики выдающийся русский ученый-механик, создатель кафедры теоретической механики в ИМТУ Николай Егорович Жуковский (1847-1921), который своими математическими исследованиями оказал влияние на развитие научной школы математики, в том числе в области качественной теории дифференциальных уравнений.
В своей магистерской диссертации «Кинематика жидкого тела», опубликованной в т. 8 «Математического сборника» (1876), при рассмотрении некоторых случаев плоскопараллельного движения несжимаемой жидкости он ввел классификацию особых точек дифференциальных уравнений первого порядка, которая содержала все четыре основных вида особых точек («узел», «седло», «фокус», «центр»), систематизированных затем в работах одного из признанных создателей качественной теории дифференциальных уравнений французского математика А.Пуанкаре.
Н.Е.Жуковский также исследовал поведение интегральных кривых в окрестности особой точки каждого вида. Однако это направление исследований, являвшееся лишь ответвлением его работ по механике, в дальнейшем не получило продолжения. Но авторитет Н.Е.Жуковского в развитии качественной теории дифференциальных уравнений был настолько высок, что в 1892 г. он выступил в Московском университете оппонентом на защите А.М.Ляпуновым докторской диссертации «Общая задача об устойчивости движения», в значительной мере определившей основные идеи и методы последующих работ в этой области.
Глубокая и взаимно обогащающая связь научных исследований по математике и механике, ярко проявившаяся в работах Н.Е.Жуковского, была характерна для научных школ этих направлений. Например, решение им задачи определения гидродинамических сил, в том числе подъемной силы при обтекании крыла воздушным потоком, в значительной мере повлияло на развитие разделов теории функций комплексного переменного, связанных с методами конформных отображений. Следует отметить, что за работу «О прочности движения» Н.Е.Жуковский в 1882 г. получил ученую степень доктора прикладной математики. Признанием авторитета Н.Е.Жуковского в области математики явилось избрание его в 1905 г. президентом Московского математического общества, постоянным членом которого он состоял с 1876 г.
 Преподававший в ИМТУ в 1896-1906 гг. на кафедре теоретической механики его ученик, один из основоположников современной гидроаэродинамики, академик Сергей Алексеевич Чаплыгин (1869-1942) разработал приближенный метод интегрирования обыкновенных дифференциальных уравнений первого порядка и их систем, вошедший затем в математическую литературу под названием метода Чаплыгина.
Преподававший в ИМТУ в 1896-1906 гг. на кафедре теоретической механики его ученик, один из основоположников современной гидроаэродинамики, академик Сергей Алексеевич Чаплыгин (1869-1942) разработал приближенный метод интегрирования обыкновенных дифференциальных уравнений первого порядка и их систем, вошедший затем в математическую литературу под названием метода Чаплыгина.
В 1896 году начал свою работу на кафедре Евгений Александрович Болотов (1870-1922), известный математик и механик, выпускник Казанского университета. Его научные исследования относятся главным образом к аналитической механике. В 1907 г. Е.А. Болотов был утвержден в степени магистра прикладной математики за работу на тему «О движении материальной плоской фигуры, стесненной связями с трением». В своем отзыве на эту работу Н.Е. Жуковский отметил, что главная заслуга Болотова в этой работе – его геометрический анализ.
 Самой значительной работой Болотова по аналитической механике является его исследование наиболее общего вариационного принципа механики – принципа наименьшего принуждения Гаусса. Е.А. Болотову принадлежит обобщение принципа наименьшего принуждения, которое легло в основу дальнейших исследований этого принципа учеными казанской школы механики. Представляют также интерес работы Болотова по гидромеханике и учебные руководства по курсам математического анализа и аналитической геометрии, которые ученый много лет читал в Московском техническом училище. В училище он читал курс аналитической геометрии и одновременно вел упражнения по теоретической и аналитической механике, которую читал Н.Е. Жуковский.
Самой значительной работой Болотова по аналитической механике является его исследование наиболее общего вариационного принципа механики – принципа наименьшего принуждения Гаусса. Е.А. Болотову принадлежит обобщение принципа наименьшего принуждения, которое легло в основу дальнейших исследований этого принципа учеными казанской школы механики. Представляют также интерес работы Болотова по гидромеханике и учебные руководства по курсам математического анализа и аналитической геометрии, которые ученый много лет читал в Московском техническом училище. В училище он читал курс аналитической геометрии и одновременно вел упражнения по теоретической и аналитической механике, которую читал Н.Е. Жуковский.
В лекциях по аналитической геометрии Болотов излагал аналитическую геометрию на плоскости и в пространстве, а также сферическую тригонометрию, увязывая многие разделы этого курса с отдельными вопросами теоретической механики и астрономии.
Е.А. Болотов уделял большое внимание подготовке своих лекций. Он обрабатывал их настолько детально и тщательно, что при издании их почти не требовалось редактировать.
С 1914 по 1921 гг. Е.А. Болотов заведовал кафедрой теоретической механики Казанского университета, а в 1921-1922 – кафедрой теоретической механики ИМТУ.
 На формирование научной школы математики в училище не могла не оказать влияния деятельность выдающегося русского математика и механика академика Пафнутия Львовича Чебышева (1821-1894), у которого с преподавателями училища были давние дружеские отношения, несмотря на то, что научная жизнь ученого была связана главным образом с Санкт-Петербургом. В отчете училища за 1871 г. впервые была опубликована его работа «О центробежном уравнителе», которая явилась первым фундаментальным исследованием по теории регуляторов. В статье «О зубчатых колесах», напечатанной в 1872 г. в сборнике «Отчет и речи, произнесенные в торжественном собрании Императорского Московского технического училища 22 сентября 1872 года», он изложил аналитический метод расчета зубчатого зацепления.
На формирование научной школы математики в училище не могла не оказать влияния деятельность выдающегося русского математика и механика академика Пафнутия Львовича Чебышева (1821-1894), у которого с преподавателями училища были давние дружеские отношения, несмотря на то, что научная жизнь ученого была связана главным образом с Санкт-Петербургом. В отчете училища за 1871 г. впервые была опубликована его работа «О центробежном уравнителе», которая явилась первым фундаментальным исследованием по теории регуляторов. В статье «О зубчатых колесах», напечатанной в 1872 г. в сборнике «Отчет и речи, произнесенные в торжественном собрании Императорского Московского технического училища 22 сентября 1872 года», он изложил аналитический метод расчета зубчатого зацепления.
В последующие годы П.Л.Чебышев регулярно посещал училище, чтобы руководить изготовлением и испытаниями в механической лаборатории спроектированных им регуляторов и других механизмов и устройств. Стремление усовершенствовать шарнирный механизм, называемый параллелограммом Уатта, натолкнуло его на постановку проблемы наилучшего приближения функций, заложившей основы глубокой математической теории, значение которой оказалось существенно шире первоначальной прикладной задачи. Ему принадлежит полушутливое высказывание о взаимосвязи теории и практики: «Математика пережила ранее два периода. В первом задачи ставились богами (делосская задача об удвоении куба), во втором — полубогами (Б.Паскаль, П.Ферма). Мы вошли теперь в третий период — задачи ставит нужда (практика), причем чем задача труднее, тем плодотворнее должны быть математические методы ее решения и тем шире область их последующего применения».
 Отмеченная связь математических исследований с работами по механике и их определенная прикладная направленность прослеживаются и на последующих этапах развития научной школы математики. В 1936-1941 гг. кафедрой высшей математики заведовал д-р техн. наук, проф. Дмитрий Юрьевич Панов (1904–1975), специалист в области вычислительной математики, известный своими трудами по численному решению дифференциальных уравнений в частных производных, по нелинейной теории упругости и вибрации непризматических стержней сложного профиля.
Отмеченная связь математических исследований с работами по механике и их определенная прикладная направленность прослеживаются и на последующих этапах развития научной школы математики. В 1936-1941 гг. кафедрой высшей математики заведовал д-р техн. наук, проф. Дмитрий Юрьевич Панов (1904–1975), специалист в области вычислительной математики, известный своими трудами по численному решению дифференциальных уравнений в частных производных, по нелинейной теории упругости и вибрации непризматических стержней сложного профиля.
 Исследования в этих направлениях применительно к расчету воздушных винтов самолетов развивали в тесном контакте с ЦАГИ сотрудники кафедры Б.П. Демидович, П.М.Риз, Б.О. Солоноуц, А.Р. Янпольский.
Исследования в этих направлениях применительно к расчету воздушных винтов самолетов развивали в тесном контакте с ЦАГИ сотрудники кафедры Б.П. Демидович, П.М.Риз, Б.О. Солоноуц, А.Р. Янпольский.
 С 1936 по 1948 гг. на кафедре работал доцент (в последствие профессор) Борис Павлович Демидович (1906-1977). Основными направлениями его научной деятельности были качественная теория обыкновенных дифференциальных уравнений, математическая физика и теория функций. В своих работах (их у него около шестидесяти) Б.П. Демидович исследовал динамические системы с интегральными инвариантами, периодические и почти периодические решения, ограниченные решения обыкновенных дифференциальных уравнений, правильные и вполне правильные дифференциальные системы, устойчивость обыкновенных дифференциальных уравнений, в частности, орбитальная устойчивость динамических систем.
С 1936 по 1948 гг. на кафедре работал доцент (в последствие профессор) Борис Павлович Демидович (1906-1977). Основными направлениями его научной деятельности были качественная теория обыкновенных дифференциальных уравнений, математическая физика и теория функций. В своих работах (их у него около шестидесяти) Б.П. Демидович исследовал динамические системы с интегральными инвариантами, периодические и почти периодические решения, ограниченные решения обыкновенных дифференциальных уравнений, правильные и вполне правильные дифференциальные системы, устойчивость обыкновенных дифференциальных уравнений, в частности, орбитальная устойчивость динамических систем.
 С 1946 по 1961 гг. на кафедре работал д.ф.-м.н., профессор Петр Михайлович Риз (1902-1990). Он занимался такими проблемами как вопросы прочности в самолетостроении, теория случайных процессов, фундаментальные проблемы теории упругости. Его работы по математике и механике всегда отличались исключительной ясностью, глубиной исследований и одновременно краткостью изложения. П.М. Риз долгое время читал лекции для аспирантов и сотрудников института по совершенно различным разделам математики и механики, как, например, «Теория случайных процессов», «Теория нелинейных колебаний», «Исследование операций», «Методы функций в гидро- и аэродинамике».
С 1946 по 1961 гг. на кафедре работал д.ф.-м.н., профессор Петр Михайлович Риз (1902-1990). Он занимался такими проблемами как вопросы прочности в самолетостроении, теория случайных процессов, фундаментальные проблемы теории упругости. Его работы по математике и механике всегда отличались исключительной ясностью, глубиной исследований и одновременно краткостью изложения. П.М. Риз долгое время читал лекции для аспирантов и сотрудников института по совершенно различным разделам математики и механики, как, например, «Теория случайных процессов», «Теория нелинейных колебаний», «Исследование операций», «Методы функций в гидро- и аэродинамике».
 В 1953-1958 гг. кафедру возглавлял д-р техн. наук, проф. Кирилл Петрович Станюкович (1916-1989), выдающийся физик-теоретик, астроном, газодинамик, заслуженный деятель науки и техники РСФСР. Всего им опубликовано более 600 научных работ. Он занимался проблемами метеорной астрономии, кратерообразования на Луне и планетах, вопросами гравитации, космогонии и космологии. В области газовой динамики изучал неустановившиеся движения сплошной среды, взрывные явления, проблемы космической газодинамики. В области теоретической физики – теорию гравитации и элементарных частиц. Его работы сыграли заметную роль в развитии ряда научных направлений в газовой динамике, теории детонации, релятивистской механике сплошной среды.
В 1953-1958 гг. кафедру возглавлял д-р техн. наук, проф. Кирилл Петрович Станюкович (1916-1989), выдающийся физик-теоретик, астроном, газодинамик, заслуженный деятель науки и техники РСФСР. Всего им опубликовано более 600 научных работ. Он занимался проблемами метеорной астрономии, кратерообразования на Луне и планетах, вопросами гравитации, космогонии и космологии. В области газовой динамики изучал неустановившиеся движения сплошной среды, взрывные явления, проблемы космической газодинамики. В области теоретической физики – теорию гравитации и элементарных частиц. Его работы сыграли заметную роль в развитии ряда научных направлений в газовой динамике, теории детонации, релятивистской механике сплошной среды.
В 1959 г. кафедрой заведовал д-р техн. наук, проф. И.А.Паничкин, научные работы которого были посвящены вопросам обтекания тел вращения высокоскоростным воздушным потоком. Руководивший кафедрой в 1960-1965 гг. д-р техн. наук, проф. Н.К.Куликов разрабатывал методы решения систем обыкновенных дифференциальных уравнений с переменными коэффициентами, описывающих сложные динамические устройства, в том числе системы автоматического регулирования.
В 1966-1970 гг. заведующим кафедрой был д-р физ.-мат. наук, проф. Дюис Данилович Ивлев, известный своими работами по математической теории идеальной пластичности, предельному равновесию оболочек вращения и теории упрочняющегося пластического тела. Автор более 120 научных трудов, среди которых монографии «Теория идеальной пластичности», «Теория уплотняющегося пластического тела», «Метод возмущений теории упруго-пластичного тела», 30 авторских свидетельств на изобретения.
Высокий уровень математических исследований прикладного характера в МВТУ базировался на прочном теоретическом фундаменте, в создании которого на кафедре высшей математики училища участвовали многие видные математики, в том числе профессора Московского университета С.П. Фиников, А.Я. Хинчин, А.О. Гельфонд, Л.А.Тумаркин, работавшие в училище в сравнительно молодом возрасте, в период своего научного расцвета.
 В конце 19 – начале 20 века на кафедре работал Леонид Кузьмич Лахтин (1863-1927), российский математик, специалист в области решения алгебраических уравнений высших степеней, а также в области математической статистики. Заслуженный профессор Московского университета, ректор Московского университета (1904—1905), декан Физико-математического факультета Московского университета (1912—1918). Его магистерская диссертация «Алгебраические уравнения, разрешимые в гипергеометрических функциях» посвящена исследованию уравнений 3-й, 4-й, 5-й и одного вида 6-й степени. В 1897 году он защитил докторскую диссертацию «Дифференциальные резольвенты алгебраических уравнений высших родов».
В конце 19 – начале 20 века на кафедре работал Леонид Кузьмич Лахтин (1863-1927), российский математик, специалист в области решения алгебраических уравнений высших степеней, а также в области математической статистики. Заслуженный профессор Московского университета, ректор Московского университета (1904—1905), декан Физико-математического факультета Московского университета (1912—1918). Его магистерская диссертация «Алгебраические уравнения, разрешимые в гипергеометрических функциях» посвящена исследованию уравнений 3-й, 4-й, 5-й и одного вида 6-й степени. В 1897 году он защитил докторскую диссертацию «Дифференциальные резольвенты алгебраических уравнений высших родов».
В 1924 году Л.К. Лахтин опубликовал большой учебник по теории вероятностей.
 Известный специалист в области дифференциальной геометрии Сергей Павлович Фиников (1883-1964), работая на кафедре с 1913 г., в 1920-е годы возглавлял математическую подготовку на инженерно-строительном и электромеханическом факультетах МВТУ. Первые работы С.П. Финикова посвящены поиску главных оснований для заданного линейного элемента поверхности. Им исследовано изгибание поверхностей на кинематическом основании. Он был одним из первых геометров, перешедших в своих исследованиях на метод внешних дифференциальных форм. С.П. Фиников сыграл большую роль в распространении идей и методов Картана. В 1948 году вышла его монография «Метод внешних форм Картана», в которой наряду с изложением теории Картана, а также работ Рикье и Томаса, изложены методы определения характеристических многообразий и особых решений систем дифференциальных уравнений.
Известный специалист в области дифференциальной геометрии Сергей Павлович Фиников (1883-1964), работая на кафедре с 1913 г., в 1920-е годы возглавлял математическую подготовку на инженерно-строительном и электромеханическом факультетах МВТУ. Первые работы С.П. Финикова посвящены поиску главных оснований для заданного линейного элемента поверхности. Им исследовано изгибание поверхностей на кинематическом основании. Он был одним из первых геометров, перешедших в своих исследованиях на метод внешних дифференциальных форм. С.П. Фиников сыграл большую роль в распространении идей и методов Картана. В 1948 году вышла его монография «Метод внешних форм Картана», в которой наряду с изложением теории Картана, а также работ Рикье и Томаса, изложены методы определения характеристических многообразий и особых решений систем дифференциальных уравнений.
 В 1929-1930 гг. кафедрой высшей математики училища заведовал Александр Яковлевич Хинчин (1894-1959), один из создателей советской школы теории вероятностей, избранный в 1939 г. членом-корреспондентом АН СССР. Он перенес методы метрической теории функций в теорию чисел и теорию вероятностей, открыл закон повторного логарифма, заложил основы теории случайных процессов, разработал методы теории массового обслуживания, использовал методы теории вероятностей в качестве математического аппарата статистической физики. А.Я.Хинчин является автором ряда учебников и учебных пособий по математике, выдержавших по три-четыре издания, а «Элементарное введение в теорию вероятностей», написанное им в соавторстве с Б.В.Гнеденко, издавалось 9 раз.
В 1929-1930 гг. кафедрой высшей математики училища заведовал Александр Яковлевич Хинчин (1894-1959), один из создателей советской школы теории вероятностей, избранный в 1939 г. членом-корреспондентом АН СССР. Он перенес методы метрической теории функций в теорию чисел и теорию вероятностей, открыл закон повторного логарифма, заложил основы теории случайных процессов, разработал методы теории массового обслуживания, использовал методы теории вероятностей в качестве математического аппарата статистической физики. А.Я.Хинчин является автором ряда учебников и учебных пособий по математике, выдержавших по три-четыре издания, а «Элементарное введение в теорию вероятностей», написанное им в соавторстве с Б.В.Гнеденко, издавалось 9 раз.

В 1931 г. кафедру возглавлял Александр Осипович Гельфонд (1906-1968) — специалист в области теории чисел, теории функций комплексного переменного и конечно-разностных методов. Ему удалось установить глубокие связи между аналитическими свойствами функций комплексного переменного и теорией чисел и создать аналитические методы доказательства трансцендентности чисел. В работах 1929 г. и 1934 г. им была решена седьмая проблема Гильберта о трансцендентности чисел специального вида, а затем доказан ряд теорем о взаимной трансцендентности чисел. В теории функций ему принадлежат работы по интерполированию целых функций и связи между ростом целых функций и арифметическими свойствами их значений. В 1939 г. А.О. Гельфонд был избран членом-корреспондентом АН СССР.

В 1931-1936 гг. кафедрой заведовал Лев Абрамович Тумаркин (1904-1974). У нас в стране и за рубежом он известен своими работами в области топологии, и прежде всего по теории размерности, которые публиковались начиная с 1925 г. Одним из его наиболее важных результатов является решение поставленной П.С.Урысоном проблемы о возможности разбиения компакта n-мерным подкомпактом. Л.А. Тумаркин показал, что все основные факты теории размерности, установленные в категории компактов, справедливы и вне этой категории, поскольку найденные им доказательства не используют условий компактности, а требуют лишь метризуемости пространства и наличия в нем счетной базы.
С 1930 г. на кафедре работал, а в период 1941-1952 гг. заведовал кафедрой доктор физ.-мат. наук, проф. Адольф (Андрей) Павлович Юшкевич (1906-1993) — видный историк математики, инициатор издания трудов многих классиков математики, один из основателей и ответственный редактор сборников «Историко-математические исследования», президент Международной академии истории науки (1965-1968). Он много сделал для установления тесных научных и методических связей кафедры высшей математики МВТУ с ведущими математическими кафедрами вузов страны, что способствовало высокому уровню научных исследований и преподавания математики в училище.
 Влияние научного потенциала кафедры высшей математики на качество математической подготовки в училище и на уровень методического обеспечения математических курсов прослеживается, начиная с деятельности А.В. Летникова. В 1888 г. кафедру возглавил проф. Николай Александрович Шапошников (1851-1920), курсы лекций которого были для своего времени образцовыми, а составленные им учебные пособия долгое время являлись основными почти во всех технических вузах России. Он, как и А.В.Летников, интересовался вопросами методики преподавания элементарной математики и ее связью с методикой преподавания высшей математики. Н.А.Шапошников являлся автором ряда учебников по элементарной и высшей математике («Курс арифметики», «Основания общей арифметики и алгебры», «Основания теории детерминантов», «Курс тригонометрии», «Алгебра», «Основной курс математического анализа»), а составленный им в соавторстве с Н.К.Вальцевым «Методический сборник алгебраических задач» выдержал с 1887 г. по 1917 г. 24 издания, а после 1917 г. — еще 28 изданий.
Влияние научного потенциала кафедры высшей математики на качество математической подготовки в училище и на уровень методического обеспечения математических курсов прослеживается, начиная с деятельности А.В. Летникова. В 1888 г. кафедру возглавил проф. Николай Александрович Шапошников (1851-1920), курсы лекций которого были для своего времени образцовыми, а составленные им учебные пособия долгое время являлись основными почти во всех технических вузах России. Он, как и А.В.Летников, интересовался вопросами методики преподавания элементарной математики и ее связью с методикой преподавания высшей математики. Н.А.Шапошников являлся автором ряда учебников по элементарной и высшей математике («Курс арифметики», «Основания общей арифметики и алгебры», «Основания теории детерминантов», «Курс тригонометрии», «Алгебра», «Основной курс математического анализа»), а составленный им в соавторстве с Н.К.Вальцевым «Методический сборник алгебраических задач» выдержал с 1887 г. по 1917 г. 24 издания, а после 1917 г. — еще 28 изданий.
Одним из лучших исследований Н.А.Шапошникова является оригинальная работа «Интегрирование дифференциальных уравнений с полными дифференциалами и частными производными первого порядка», содержащая достаточно общий прием упрощения исходного уравнения и сведения его к стандартному виду. Под руководством Н.А.Шапошникова профессорами кафедры были подготовлены и изданы важнейшие курсы: «Курс аналитической геометрии» К.А.Андреева, «Анализ и аналитическая геометрия» Д.Н.Горячева, «Математический анализ» Е.А.Болотова, курсы по аналитической геометрии Л.К.Лахтина.
Вот что вспоминал об этом времени выпускник, а позднее профессор, заведующий кафедрой теоретической механики В.П.Ветчинкин: «После ухода из МТУ преподавателя Н.А.Шапошникова Е.А. Болотов занял его кафедру высшего анализа, передав кафедру аналитической геометрии заслуженному профессору К.А.Андрееву. Несмотря на это, еще долгое время основным руководством для студентов по аналитической геометрии служил литографированный курс Е.А. Болотова.»
Что касается курса математического анализа, то учебник Н.А.Шапошникова (достаточно полный, но сухой по изложению и несколько трудный для понимания) быстро был вытеснен двухтомным литографированным курсом Е.А.Болотова, который отличался оригинальностью изложения и содержал важные для практических приложений сведения — например, вывод весьма удобной формулы квадратур Понселе, которого не присутствуют ни в одном из курсов анализа других авторов, русских и иностранных, есть более 30 таких курсов — как общих, так и специально посвященных приближенным вычислениям.
В годы революции Н.А. Шапошников, уже вышедший на пенсию, оказался в Геленджике, где преподавал в женской гимназии. В сентябре 1918 он был приглашен Б.Л. Розингом в Екатеринодар (ныне Краснодар), где стал ректором только что открывшегося Северо-Кавказского политехнического института и его профессором математики. Н.А. Шапошников отстаивал сохранение СКПИ, когда над ним нависла угроза закрытия со стороны белоказачьих властей, в частности, в своей статье «Два законопроекта», опубликованной газетой «Кубанский край» (15 ноября 1918).
После 1917 г. кафедра высшей математики МВТУ играла заметную роль в организации и совершенствовании математического образования в вузах страны. В 1920-х годах при унификации в стране учебных планов подготовки инженеров-механиков по курсу высшей математики за основу был принят учебный план механического факультета МВТУ, представленный и обоснованный деканом этого факультета И.И.Куколевским. В период введения в учебный процесс всевозможных неопробированных новаций научно-педагогическая общественность училища настояла на сохранении лекционной формы обучения, в том числе по математике и другим общенаучным дисциплинам. Представители кафедры активно участвовали в многочисленных дискуссиях по проблемам преподавания математики в вузах (см., например, журналы «Естествознание и марксизм», 1930, №2,3 и «Вестник высшей школы», 1941, № 5) и последовательно отстаивали свои позиции. Научно-методические работы преподавателей кафедры регулярно публиковались в сборниках трудов, издававшихся в МВТУ.
Накопленные на кафедре в процессе преподавания методические материалы после тщательного отбора и длительной апробации использовались в многочисленных учебных пособиях для студентов. В частности, опыт ведения практических занятий по математике был обобщен в изданном в 1944 г. в МВТУ «Задачнике по высшей математике», подготовленном большим коллективом преподавателей кафедры, в который входил и погибший в декабре 1941 г. в ополчении С.Ф.Шурлапов. Этот задачник выдержал четыре издания и на его основе был составлен в 1959 г. под редакцией проф. Б.П.Демидовича сборник «Задачи и упражнения по математическому анализу для втузов». Сборник содержал более 3000 задач по всем основным разделам втузовского курса математики (за исключением аналитической геометрии) с ответами, методическими указаниями и решениями типовых примеров. Он переиздавался десять раз, был переведен на французский, испанский и португальский языки. Его авторами были преподаватели, в разное время работавшие на кафедре высшей математики МВТУ: Г.С.Бараненков, Б.П.Демидович, В.А.Ефименко, С.М.Коган, Г.Л.Лунц, Е.Ф.Поршнева, Е.П.Сычева, С.В.Фролов, Р.Я.Шостак, А.Р.Янпольский.
Длительный период методического совершенствования математической подготовки будущих инженеров в МВТУ был отражен в написанном доцентами кафедры Сергеем Васильевичем Фроловым и Родионом Яковлевичем Шостаком «Курсе высшей математики», выпущенном двумя изданиями (в 1966 г. и 1973 г.), а в 1968 г. вышло учебное пособие Р.Я.Шостака по операционному исчислению.
В 1973 г. из состава кафедры высшей математики выделилась кафедра прикладной математики, которую возглавил лауреат Государственной премии СССР д-р техн. наук, проф. Р.С.Судаков.
 Кафедру «Высшая математика» возглавил д-р физ.мат. наук, проф. Михаил Сергеевич Яров-Яровой (1929–2004) известный математическими работами в области небесной механики, математики и численного интегрирования. Он разработал аналитическую теорию полетов космического корабля к Луне, выполнил исследование движения больших планет, провел численное интегрирование уравнений движений по уточненным формулам с использованием высших производных от решения, вывел новые представления потенциала небесных тел в эллипсоидальных координатах.
Кафедру «Высшая математика» возглавил д-р физ.мат. наук, проф. Михаил Сергеевич Яров-Яровой (1929–2004) известный математическими работами в области небесной механики, математики и численного интегрирования. Он разработал аналитическую теорию полетов космического корабля к Луне, выполнил исследование движения больших планет, провел численное интегрирование уравнений движений по уточненным формулам с использованием высших производных от решения, вывел новые представления потенциала небесных тел в эллипсоидальных координатах.
Современная история кафедры «Высшая математика»
 В 1976 г. кафедру «Высшая математика» возглавил Геннадий Дмитриевич Карташов (1938–2008), заслуженный деятель науки Российской Федерации, крупный специалист в области ускоренных испытаний технических систем на надежность. Его кандидатская диссертация была посвящена решению проблемы восстановления многомерной функции распределения по ее известным маргинальным распределениям (если это возможно) или в оценке ее некоторых характеристик. В 1980 году Г.Д. Карташов защитил докторскую диссертацию «Исследование проблемы инвариантности в теории форсированных испытаний», в которой заложил основы теории ускоренных испытаний в нашей стране. Г.Д. Карташову удалось решить ряд сложных задач, возникающих в различных областях теории надёжности. В частности, им решена проблема планирования экспериментов с ненаблюдаемыми одновременно случайными величинами, проблема инвариантности в теории надёжности, установления области применимости различных моделей расходования ресурса изделий. На основе полученных теоретических результатов при помощи метода вложенных множеств Карташовым Г.Д.разработан новый подход к прогнозированию надежности изделий. В отличие от традиционного – аппроксимации реализаций изменения технических параметров по времени – предложена аппроксимация по ансамблю. Для последовательных систем, состоящих из большого количества разнотипных элементов, предложены приближенные асимптотические методы форсированных испытаний. Показано, в частности, что для дискретных систем асимптотически выполняется модель Пальмгрена-Майнера (линейного суммирования повреждений) и форсированные испытания таких систем можно проводить в рамках линейной модели, если отказы элементов полные. Г. Д. Карташов – автор более 250 работ, среди которых монографии: Г.Д.Карташов «Принципы расходования ресурса и их использование для оценки надежности» (1984); А.И.Перроте, Г.Д.Карташов, К.Н. Цветаев «Основы ускоренных испытаний радиоэлементов на надежность» (1968); Г.Д. Карташов «Ускоренные испытания элементов и систем» (1990), а также государственных стандартов. Под руководством Г.Д.Карташова было подготовлено и защищено 18 кандидатских и 4 докторских диссертаций.
В 1976 г. кафедру «Высшая математика» возглавил Геннадий Дмитриевич Карташов (1938–2008), заслуженный деятель науки Российской Федерации, крупный специалист в области ускоренных испытаний технических систем на надежность. Его кандидатская диссертация была посвящена решению проблемы восстановления многомерной функции распределения по ее известным маргинальным распределениям (если это возможно) или в оценке ее некоторых характеристик. В 1980 году Г.Д. Карташов защитил докторскую диссертацию «Исследование проблемы инвариантности в теории форсированных испытаний», в которой заложил основы теории ускоренных испытаний в нашей стране. Г.Д. Карташову удалось решить ряд сложных задач, возникающих в различных областях теории надёжности. В частности, им решена проблема планирования экспериментов с ненаблюдаемыми одновременно случайными величинами, проблема инвариантности в теории надёжности, установления области применимости различных моделей расходования ресурса изделий. На основе полученных теоретических результатов при помощи метода вложенных множеств Карташовым Г.Д.разработан новый подход к прогнозированию надежности изделий. В отличие от традиционного – аппроксимации реализаций изменения технических параметров по времени – предложена аппроксимация по ансамблю. Для последовательных систем, состоящих из большого количества разнотипных элементов, предложены приближенные асимптотические методы форсированных испытаний. Показано, в частности, что для дискретных систем асимптотически выполняется модель Пальмгрена-Майнера (линейного суммирования повреждений) и форсированные испытания таких систем можно проводить в рамках линейной модели, если отказы элементов полные. Г. Д. Карташов – автор более 250 работ, среди которых монографии: Г.Д.Карташов «Принципы расходования ресурса и их использование для оценки надежности» (1984); А.И.Перроте, Г.Д.Карташов, К.Н. Цветаев «Основы ускоренных испытаний радиоэлементов на надежность» (1968); Г.Д. Карташов «Ускоренные испытания элементов и систем» (1990), а также государственных стандартов. Под руководством Г.Д.Карташова было подготовлено и защищено 18 кандидатских и 4 докторских диссертаций.
В 1997 году было проведено еще одно разделение кафедры «Высшая математика». На ее основе была образована новая кафедра «Вычислительная математика и математическая физика», которую возглавил профессор Грешилов А. А. Кафедрой «Высшая математика» продолжал до самой смерти заведовать Карташов Г. Д.
 В 2008 году кафедру возглавил доктор технических наук, профессор Сидняев Николай Иванович. Сидняев Н.И. закончил Московский государственный технический университет им. Н.Э. Баумана, Московский государственный университет им. М.В.Ломоносова, аспирантуру при Московском государственном техническом университете им. Н.Э.Баумана и без отрыва от производства Академию народного хозяйства при Правительстве Российской Федерации. Автор более 200 научных трудов.
В 2008 году кафедру возглавил доктор технических наук, профессор Сидняев Николай Иванович. Сидняев Н.И. закончил Московский государственный технический университет им. Н.Э. Баумана, Московский государственный университет им. М.В.Ломоносова, аспирантуру при Московском государственном техническом университете им. Н.Э.Баумана и без отрыва от производства Академию народного хозяйства при Правительстве Российской Федерации. Автор более 200 научных трудов.
Сидняев Н.И. стажировался в ЦНИИМаш, ЦАГИ им. Н.Е. Жуковского, НПО им. Лавочкина, Институте Механики МГУ им. М.В. Ломоносова, Ecole Centrale de Lyon, l’Université Sorbonne (France). Занимался научно-исследовательской работой по оборонной тематике. Направления: аэромеханика, газовая динамика многофазных сред, механика жидкости газа и плазмы, прикладная механика, динамика полета и управления, прочностные расчеты, численные методы, разработка программных комплексов.
Руководил научно-исследовательскими темами и направлениями по отраслям машиностроения, авиационно-космической, металлургической и атомной промышленности (математическое моделирование, численные расчеты разработка устройств различного назначения и внедрение в производство). Работал с зарубежными и с отечественными фирмами по выполнению НИР. Работал по грантам Российского Фонда Фундаментальных Исследований (РФФИ), Минобразования и ряда ведомств. В настоящее время руководит Правительственной темой между МГТУ им. Н.Э. Баумана и ОАО «ГАЗПРОМ», по созданию комплекса новейших методик и программ, необходимых для вовлечения в разработку углеводородного сырья. Под его руководством подготовлена и разработана образовательная программа для госкорпорации «РОСНАНО». Сидняев Н.И. активно работал в рабочей группе аппарата правительства РФ. Занимался экспертизой документов для проектов Законов РФ.
 Одно из научных направлений Сидняева Н.И. – это взаимодействия газовых сред с обтекаемыми телами. В последние десятилетия эти исследования были сосредоточены в основном на двух направлениях. Первое связано с математическим моделированием обтекания высокоскостных летательных аппаратов, второе – с научными разработками в области фундаментальных проблем сверхзвуковых и гиперзвуковых течений газа. Изучены следующие проблемы: обтекание профилей дозвуковым и трансзвуковым потоком и вычисление аэродинамических коэффициентов; обтекание профиля в системе крыла и учет взаимного влияния элементов компоновки; решение обратных задач газодинамики для определения профиля по заданным распределениям нагрузки или скорости потока по его поверхности; расчет пограничного слоя в условиях ламинарно-турбулентного обтекания с вычислением точки перехода; обтекание профилей с усложненными свойствами; расчет аэродинамических характеристик различных тел при внесении конструктивных изменений и вариациях положения элементов компоновки; оптимизация профиля.
Одно из научных направлений Сидняева Н.И. – это взаимодействия газовых сред с обтекаемыми телами. В последние десятилетия эти исследования были сосредоточены в основном на двух направлениях. Первое связано с математическим моделированием обтекания высокоскостных летательных аппаратов, второе – с научными разработками в области фундаментальных проблем сверхзвуковых и гиперзвуковых течений газа. Изучены следующие проблемы: обтекание профилей дозвуковым и трансзвуковым потоком и вычисление аэродинамических коэффициентов; обтекание профиля в системе крыла и учет взаимного влияния элементов компоновки; решение обратных задач газодинамики для определения профиля по заданным распределениям нагрузки или скорости потока по его поверхности; расчет пограничного слоя в условиях ламинарно-турбулентного обтекания с вычислением точки перехода; обтекание профилей с усложненными свойствами; расчет аэродинамических характеристик различных тел при внесении конструктивных изменений и вариациях положения элементов компоновки; оптимизация профиля.
В области фундаментальных проблем высокоскоростных течений газа значительное внимание Сидняевым Н.И. уделялось вопросам совершенствования формы быстро летящих тел с целью достижения оптимальных значений аэродинамических характеристик в условиях разрушения поверхности. Сидняевым Н.И. проведены в широкие теоретические и экспериментальные исследования в области сверх- и гиперзвукового обтекания оптимальных пространственных тел, включающих изучение структуры возмущенного течения, свойств аэродинамических характеристик при различных режимах полета и наборах геометрических параметров и создание на этой основе достаточно простых и эффективных моделей расчета, позволяющих с достаточной точностью получать оценки аэродинамического сопротивления указанных тел и проводить их оптимизацию.
Теоретически в рамках модели идеальной жидкости и экспериментально с использованием различных методов, в том числе – специального оптического метода для изучения невидимых течений. В частности, теоретически обнаружены и получили экспериментальное подтверждение топологически новые структуры конических линий тока с особенностями в ударном слое при наличии маховской конфигурации ударных волн. Показано, что при их реализации нагрузка на угловую конфигурацию в окрестности режимов обтекания с плоскими ударными волнами, лежащими в плоскости передних кромок и принадлежащими на передних кромках к сильному семейству, терпит разрыв. Построены новые типы ударных волн в конических течениях с висячими скачками уплотнения, обнаруженные в эксперименте. Обнаружены режимы автоколебаний, обусловленные отрывом пограничного слоя.
Исследовано взаимодействие ударных волн с турбулентным пограничным слоем в конических течениях и его влияние на структуру течения в ударном слое и режимы обтекания. Установлена фундаментальная общность свойств отрыва турбулентного пограничного слоя в конических и плоских потоках. Построены эмпирические соотношения, позволяющие определять положение и размер области отрыва турбулентного пограничного слоя для широкого круга типов взаимодействия конических ударных волн и систем скачков уплотнения с пограничным слоем, а также прогнозировать глобальную перестройку структуры течения в конических угловых конфигурациях. Эти результаты значительно опережают соответствующие зарубежные исследования.
Определена роль каждого из параметров геометрии в снижении сопротивления сложных тел по сравнению с эквивалентными телами вращения. Определена область изменения параметров, где сложные тела обладают значительно меньшим полным сопротивлением по сравнению с эквивалентными конусами и оптимальными степенными телами вращения. Определена область ее справедливости для характерных параметров геометрии тела и различного состояния пограничного слоя, в которой модель может быть эффективно использована для постановки и решения оптимизационных задач.
Решена проблема устойчивости полета пространственных тел, с учетом известных способов стабилизации, которая потребовала изучения ряда фундаментальных вопросов: о положении центра давления пространственных тел и его зависимости от условий полета; о возможности создания компоновок, обладающих запасом статической устойчивости без использования дополнительных стабилизирующих устройств, значительно снижающих преимущество в сопротивлении по сравнению с эквивалентными телами вращения; об аэродинамике оптимальных пространственных форм при их стабилизации вращением. Впервые поставлена задача о форме конических тел в сверхзвуковом потоке, положение центра давления которых не зависит от числа Маха и угла атаки. Найдены точные и приближенные решения, представляющие практический интерес. Построена теория конических тел, обладающих максимальным запасом статической устойчивости при различных изопериметрических условиях. Получено экспериментальное подтверждение результатов теории, в том числе обнаруженного закона подобия, что позволяет рекомендовать найденные пространственные конфигурации в качестве формы устойчивого сверхзвукового летательного аппарата с малым сопротивлением и высокими несущими свойствами, обеспечивающими быстрое затухание колебаний тела около центра масс. Построена теория оптимальных пространственных тел минимального волнового сопротивления, вращающихся в гиперзвуковом потоке. Кроме исследований, связанных с выбором оптимальных форм аппаратов, летящих с большой скоростью, Сидняевым Н.И. выполнен цикл работ по сверхзвуковому обтеканию источников тепловыделения, а также развита линейная теория обтекания осесимметричных тел в условиях поверхностного массообмена, изучено обтекание затупленных тел в широком диапазоне скоростей набегающего потока.
С использованием аналитических и численных методов выявлены новые физические эффекты взаимодействия газа с источником тепломассообмена, сформулированы новые принципы формирования сверхзвуковых потоков с нужными для приложений свойствами, проведены расчеты влияния массоподвода на аэродинамические характеристики быстро летящих тел. Показана возможность эффективного управления параметрами теплообмена с помощью двухфазного вдува на обтекаемой поверхности. Предложен новый лагранжев метод расчета течений сред, описываемых уравнениями континуума без собственных напряжений. Метод основан на привлечении дополнительных уравнений для компонент якобиана перехода от эйлеровых к лагранжевым переменным, тем самым позволяя рассчитывать все параметры среды (включая плотность) из решения обыкновенных дифференциальных уравнений на фиксированных траекториях.
Исследования по механике вязких жидкостей развиваются Сидняевым Н.И., главным образом, по трем направлениям: пограничный слой, гидродинамическая неустойчивость и переход к турбулентности, развитие и приложение численных методов к решению уравнений Навье-Стокса, Эйлера, Прандтля. В течение многих лет эти исследования проводились в связи с запросами развития аэрокосмической техники, в частности, тепловой защиты летательных аппаратов. Основу многих исследований составили работы Н.И.Сидняева по гидродинамической устойчивости аэродинамических следов, вихревых слоев и течений в каналах. Что касается численных решений задач вязкой жидкости, то исследования в этом направлении всегда были связаны с идеей об особой эффективности прямых методов Галеркина в комбинации с конечноразностными процедурами. Один из таких подходов, известный как метод Галеркина-Петрова, оказался особенно полезным не только для решения линейных задач устойчивости, но и для анализа нелинейных колебательных и волновых процессов в течениях вязкой жидкости.
 Обширный цикл работ по гидродинамике вязких жидкостей на кафедре выполнен под руководством проф. Н.И.Сидняева. Продолжались традиционные для кафедры исследования фундаментальных свойств вязких потоков, дисперсных сред таких, как неустойчивость и переход к турбулентности, вихреобразование и перенос завихренности при обтекании тел конечных размеров, отрывы и автоколебания в зонах отрыва, образование и динамика поверхностей раздела и свободных поверхностей в вязких потоках, перестройки потока под воздействием внешних объемных и поверхностных сил. Выбор конкретных задач определялся актуальными запросами современной технологии, экологии, техники. Значительная часть проводимых исследований посвящена течениям со свободными поверхностями и с поверхностями раздела, в частности, капиллярным течениям в струях и пленках при различной геометрии удерживающих и формирующих поток твердых поверхностей.
Обширный цикл работ по гидродинамике вязких жидкостей на кафедре выполнен под руководством проф. Н.И.Сидняева. Продолжались традиционные для кафедры исследования фундаментальных свойств вязких потоков, дисперсных сред таких, как неустойчивость и переход к турбулентности, вихреобразование и перенос завихренности при обтекании тел конечных размеров, отрывы и автоколебания в зонах отрыва, образование и динамика поверхностей раздела и свободных поверхностей в вязких потоках, перестройки потока под воздействием внешних объемных и поверхностных сил. Выбор конкретных задач определялся актуальными запросами современной технологии, экологии, техники. Значительная часть проводимых исследований посвящена течениям со свободными поверхностями и с поверхностями раздела, в частности, капиллярным течениям в струях и пленках при различной геометрии удерживающих и формирующих поток твердых поверхностей.
Большой интерес представляют исследования Сидняева Н.И. по изучению свойств нелинейных, и особенно, сильно нелинейных волн в вязкой жидкости в условиях, когда они развиваются под воздействием сил давления в грунтах, силы тяжести и внешних воздействий. Исследование их с применением прямых методов приводит к нелинейным математическим моделям с диссипацией и дисперсией. Объект исследования составляют пограничные слои, ограниченные свободными поверхностями, и пограничные слои вблизи поверхностей раздела. Для адекватного описания движений свободной поверхности с большой амплитудой, например, сильно нелинейных волн, разработан способ соответствующего обобщения уравнений Прандтля. Выполнен большой цикл работ по аэрогидромеханике. Такие исследования включают: решение уравнений Навье-Стокса в приближении пограничного слоя для течений сред со свободными границами и границами раздела, исследование гидродинамической неустойчивости стационарных и нестационарных течений, анализ нелинейного развития возмущений и формирование волн.
Установлен ряд закономерностей фундаментального характера. Роль вязкости, формирующей профиль скорости в слое, оказывается существенной, т.к. может приводить к появлению профильной неустойчивости, отличной от неустойчивости Релея и Кельвина-Гельмгольца. Исследованы струйные течения, в которых развитием неустойчивости можно достаточно эффективно управлять с помощью наложенных вращений, геометрией удерживающей поверхности и свободной пленки. Новое развитие получила задача о пограничном слое на поверхности раздела, развивающемся под воздействием трения на поверхности. Проведенные расчеты спектров неустойчивости таких пограничных слоев открыли новые моды неустойчивости и наметили направление исследований для истолкования сложной картины турбулизации поверхности. Процессы гидродинамической неустойчивости, порождающие волновые структуры на поверхности, развиваются при сравнительно небольших числах Рейнольдса. Это обстоятельство позволяет успешно применять прямые методы для изучения динамики волновых пленок жидкости. Содержательная нелинейная модель течения построена осреднением по толщине пленки системы уравнений Навье-Стокса. Проведено численное исследование уравнений течений при задании в качестве начальных условий малых гармонических волн, а также регулярных нелинейных решений. Уравнения содержат внешний параметр, возрастающий вместе с числом Рейнольдса и средней толщиной пленки. Особое внимание уделено случаю малых волновых чисел, при которых на каждом пространственном периоде квазистационарной волны имеется четко выраженный участок невозмущенной поверхности, так что регулярная волна по существу представляет уединенную волну. Установлены общие закономерности динамики развивающихся волновых фронтов, которые заключаются в следующем. Все регулярные нелинейные волновые решения, также как малые гармонические волны, неустойчивы и автоматически перестраиваются в устойчивые волновые структуры.
В течение ряда лет на кафедре проводятся исследования по теории нелинейных волн в пленках. Решению модельных уравнений Сидняевым Н.И. посвящен целый ряд оригинальных работ и обзорных статей. Разработанные Сидняевым Н.И. методы находят эффективное приложение к изучению неустойчивости и нелинейных волн, усложненных процессами тепло- и массообмена. Анализ проблем обобщения и приложений модельных уравнений показал, что часто применяемые слабонелинейные модельные уравнения являются частными случаями модельных уравнений при стремлении к нулю единственного свободного параметра подобия, отражающего условия экспериментов. Как следствие этого, нелинейные волновые решения предельных модельных уравнений представляют лишь математические волны. Проведено подробное численное исследование нестационарных решений предельного модельного уравнения и построена наиболее полная картина динамики их развития во времени. В развитие проблемы о тепломассопереносе, выполнен ряд работ, в которых основной результат обобщен на другие случаи. В связи с нелинейностью основных уравнений численные методы играют существенную роль в аэрогидродинамике. Они применяются не только для доведения до конечного численного результата решений отдельных задач, но, главным образом, для выявления фундаментальных свойств течений. Особенно это относится к течениям вязкой жидкости. Развитие численных методов Сидняевым Н.И. ориентировано на применение прямых методов при гибком комбинировании их с методами конечных разностей. Численные методы решения линейных и нелинейных проблем гидродинамической устойчивости разрабатывались для изучения неустойчивости, нелинейного развития возмущений и переходов к сложным пространственным структурам в потоках с границами раздела и зонами отрыва, формирующихся в закрученных потоках и при обтекании плоских тел вязкой жидкостью. Исследованы критические значения параметров, при которых происходит потеря устойчивости стационарных течений, изучается нелинейный переход к новым периодическим или квазипериодическим состояниям и находятся решения уравнений Навье-Стокса для вторичных течений. В частности, решена проблема отыскания собственных чисел для системы уравнений Орра-Зоммерфельда в двух областях с условиями плавного сопряжения на границе раздела. Это создает возможность находить области неустойчивости и наиболее растущие возмущения в течениях. Численными экспериментами показано, что возможно надежное моделирование ламинарного и турбулентного закрученного течения с застойной зоной ламинарным потоком с эффективным числом Рейнольдса, которому соответствует подходящее решение уравнений Навье-Стокса. Для истолкования гидродинамических механизмов разрушения вихрей исследована неустойчивость закрученных потоков с застойной зоной, которые характеризуются тем, что основное течение не плоскопараллельное. Обнаружены новые моды для свободного вихря, изучено возникновение, исчезновение, переход мод друг в друга при изменении чисел Рейнольдса, закрутки, геометрических параметров.
Проведены исследования взаимодействий неустойчивостей и зон отрыва при обтекании профиля крыла с перфорированной и непроницаемой поверхностью дозвуковым и трансзвуковым потоком газа. Усовершенствована вычислительная схема для расчета базовой задачи об обтекании кругового цилиндра, сопровождаемым формированием нестационарной зоны отрыва с вихревой дорожкой, при учете перемещений цилиндра. Отработаны алгоритмы, программы и постановки задач, учитывающих развитие неустойчивости в пограничном слое от носика профиля до зон отрыва. Прямыми вычислениями показана возможность затягивания перехода и отрыва с помощью управляемого вдува. Включение перфорации поверхности в анализ позволяет конструировать сверхзвуковые течения, в которых зона отрыва, вызываемая размытым скачком, оказывается минимальной.
Новый нелинейный эффект обнаружен прямыми вычислениями в задаче о вторичных течениях после потери устойчивости вращающегося течения. Наряду с вихрями Тейлора, самопроизвольно развивающимися из малых возмущений, существуют также периодические структуры, которые устанавливаются при начальных возмущениях конечной амплитуды. Развиты математические модели пограничного слоя в условиях массопереноса. Широкий круг вопросов, связанных с теорией пластических деформаций, химической технологией, течениями многофазных сред, геофизикой и геологией, исследован профессором Н.И. Сидняевым, а также построена математическая модель фильтрации газа через тепловыделяющую грунтовую среду, на основе которой удалось объяснить данные наблюдений за поведением криолитозоны. Учет неньютоновских реологических свойств мантийных пород грунтов позволил воспроизвести ряд известных в геологии особенностей эволюции глобального геодинамического процесса в районах Крайнего Севера.
Кафедра «Высшая математика» сегодня
В настоящее время на кафедре «Высшая математика» работают 15 профессоров, 29 доцентов, 9 старших преподавателей, 8 ассистентов. Среди преподавателей кафедры выпускники МГУ им. М. В. Ломоносова (механико-математического, физического факультетов, факультета вычислительной математики и кибернетики), МФТИ, МГТУ им. Н. Э. Баумана, физико-математических факультетов других университетов. Более сорока лет на кафедре работают доценты Вилисова Н. Т., Крапоткин В.Г., Кузнецов В.В., Паршев Л.П., Покровский Л.Д., Янов И.О.
 Доц. Паршев Л. П. в течение многих лет возглавляет предметную комиссию по математике университета.
Доц. Паршев Л. П. в течение многих лет возглавляет предметную комиссию по математике университета.
Профсоюзный комитет кафедры возглавляет старший преподаватель Шевченко М. Н.
Доц. Крапоткин В. Г. С 1981 по 1985 г. Работал в Алжире, в институте нефтегазовой химии, а с 1985 по 1988 г. В Мали, в высшей инженерной школе.
Доц. Соболев С. К. с 1983 по 1987 г. работал в Мозамбике, заведовал кафедрой теоретической математики на математическом факультете Мозамбикского университета.
Доц. Кузнецов В. В. участвовал в создании СУНЦ (физико-математический лицей №1580 при МГТУ им. Н. Э. Баумана), а также в течение восьми лет был его директором.
Доц. Леванков В. И. в течение многих лет ведет занятия в ГУИМЦ для слабослышащих студентов.
 Доц. Кузнецов В. В. является заслуженным мастером спорта СССР, бронзовым призером Олимпийских игр 1964 года, чемпионом мира 1966 года в составе сборной СССР по водному поло. Доц. Леванков В. И. является мастером спорта по бадминтону. Доц. Крапоткин В. Г. – кандидат в мастера спорта по самбо, двукратный чемпион Москвы, проф. Васильев Н. С. – мастер спорта по спортивной гимнастике.
Доц. Кузнецов В. В. является заслуженным мастером спорта СССР, бронзовым призером Олимпийских игр 1964 года, чемпионом мира 1966 года в составе сборной СССР по водному поло. Доц. Леванков В. И. является мастером спорта по бадминтону. Доц. Крапоткин В. Г. – кандидат в мастера спорта по самбо, двукратный чемпион Москвы, проф. Васильев Н. С. – мастер спорта по спортивной гимнастике.
Проф. Смольяков Э. Р. является специалистом по нетрадиционным методам сохранения и восстановления здоровья. Об этом он написал в книге «Тайны жизни. Практика умственного и физического самосовершенствования».
Проф. Ильичев А. Т. является автором справочника по русской истории.
Научная работа
Круг научных интересов специалистов, работающих на кафедре, очень широк. По ряду направлений они занимают ведущие позиции в разрабатываемых проблемах теоретической и прикладной математики. Многие результаты, полученные преподавателями кафедры, получили признание не только в нашей стране, но и за рубежом. На кафедре работает научный семинар «Динамика возмущений в сплошных средах» под руководством профессоров А. Т. Ильичева и А. С. Савина, проводятся научные конференции по актуальным направлениям развития прикладной математики в энергетике, энергоэффективности и информационно-коммуникационных технологиях.
Основными направлениями исследований на кафедре являются:
- Дифференциальные уравнения и уравнения в частных производных (проф. Филиновский А. В., доц. Гласко А. В., доц. Зорина И. Г., доц. Неклюдов А. В., доц. Станцо В. В., доц. Копаев А. В., доц. Павельева Е. Б., доц. Покровский Л. Д., доц. Аникин А. Ю.).
- Теория вероятностей, математическая статистика, математическая теория надежности (проф. Белов В. Н., доц. Ветров Л. Г., проф. Калинкин А. В., проф. Павлов И. В., проф. Тимонин В. И., доц. Сунчалина А. Л.).
- Исследование операций (проф. Васильев Н. С., проф. Грешилов А.А., проф. Смольяков Э.Р.).
- Функциональный анализ и алгебра (проф. Исмагилов Р. С., доц. Табалдыев С. Б., доц. Храпов П. В., доц. Огнева О. С.).
- Механика сплошной среды (проф. Ильичев А.Т., проф. Савин А. С., проф. Сидняев Н. И., доц. Томашпольский В. Я., доц. Федотов А.А., проф. Шахов Е. М., доц. Богомолов В. Г., доц. Бояринцева Т. Е., доц. Янов И. О.).
- Теория атомарных и R – функций, вейвлеты, фракталы (проф. Кравченко В. Ф., ст. преп. Коновалов Я.Ю.).
Фундаментальные научные направления
1. Дифференциальные уравнения и уравнения в частных производных.
 Профессор Филиновский Алексей Владиславович, доктор физико-математических наук, крупный специалист в области уравнений математической физики. Он автор более 100 научных работ, им опубликованы 2 монографии по исследуемой тематике. Его научные результаты относятся к решению задач стабилизации при больших значениях времени решений нестационарных смешанных задач для эллиптических операторов в неограниченных областях; исследованию экстремальных задач для уравнений в частных производных; изучению спектральных свойств несамосопряженных краевых задач. Среди главных результатов:
Профессор Филиновский Алексей Владиславович, доктор физико-математических наук, крупный специалист в области уравнений математической физики. Он автор более 100 научных работ, им опубликованы 2 монографии по исследуемой тематике. Его научные результаты относятся к решению задач стабилизации при больших значениях времени решений нестационарных смешанных задач для эллиптических операторов в неограниченных областях; исследованию экстремальных задач для уравнений в частных производных; изучению спектральных свойств несамосопряженных краевых задач. Среди главных результатов:
- изучено асимптотическое поведение при больших значениях времени решений внешних краевых задач для нестационарных уравнений высокого порядка;
- получены интегральные оценки скорости убывания решений первой смешанной задачи для волнового уравнения в областях с компактными незвездными границами;
- получены равномерные по спектральному параметру оценки резольвентны первой краевой задачи для оператора Лапласа и ее производной по спектральному параметру в неограниченных областях;
- получено достаточное условие непрерывности спектра первой краевой задачи для полигармонического оператора в областях с некомпактными границами;
- изучены классы существования решений экстремальных задач с несамосопряженными краевыми условиями для параболических уравнений.
Результаты исследований частично изложены в монографиях:
- Асташова И.В., Кондратьев В.А., Муравей Л.А., Филиновский А.В. Качественная теория дифференциальных уравнений. – М.: МАТИ-РГАТУ, 2001. – 141с.
- Astashova I.V., Filinovskii A.V., Kondratiev V.A., Muravey L.A. Some Problems in Qualitative Theory of Differential Equations. – London.; Jnan Bhawan Publishers, 2002.
 Доцент Гласко Андрей Владленович, кандидат физико– математических наук, автор около 30 научных работ.
Доцент Гласко Андрей Владленович, кандидат физико– математических наук, автор около 30 научных работ.
Область научных интересов Гласко А.В. распространяется на использование уравнений математической физики для создания математических моделей, моделирующих как поведение живых систем, так и процессы самоорганизации искусственных систем (в частности, наноматериалы).
К основным результатам относятся:
- создана и частично обоснована математическая модель динамики внимания в процессе восприятия элементарного внешнего стимула;
- разработка модели конвергентных процессов, имеющей приложения в процессе описания самоорганизации материи и самосборки наноструктур, представляющих основу восходящих технологий.
Доцент Павельева Елена Борисовна, кандидат физико – математических наук, автор около 10 научных работ. Занимается исследованием асимптотических свойств решений уравнения переноса излучения в неодномерных протяженных цилиндрических областях.
На основе асимптотической теории разработаны алгоритмы поиска асимптотических режимов в протяженных неодномерных цилиндрических областях и получены тестовые результаты для радиационных полей в задачах о глубоко проникающем излучении.
 Доцент Неклюдов Алексей Владимирович, кандидат физико – математических наук. Область научных интересов – изучение поведения решений эллиптических уравнений, в т.ч. нелинейных, в неограниченных областях. Получены результаты по поведению решений задачи Неймана для уравнений произвольного порядка в областях, близких к цилиндрическим. Исследованы особенности решений в цилиндрической области нелинейного уравнения второго порядка с экспоненциальной нелинейностью. Результаты исследований опубликованы в нескольких статьях журналов АН Российской Федерации.
Доцент Неклюдов Алексей Владимирович, кандидат физико – математических наук. Область научных интересов – изучение поведения решений эллиптических уравнений, в т.ч. нелинейных, в неограниченных областях. Получены результаты по поведению решений задачи Неймана для уравнений произвольного порядка в областях, близких к цилиндрическим. Исследованы особенности решений в цилиндрической области нелинейного уравнения второго порядка с экспоненциальной нелинейностью. Результаты исследований опубликованы в нескольких статьях журналов АН Российской Федерации.
 Доцент Станцо Виталий Владимирович, кандидат физико–математических наук. Он является специалистом по качественной теории дифференциальных уравнений. Его исследования посвящены исследованию возникновения предельных циклов в трехпараметрических двумерных динамических системах. В частности, ему принадлежит результат, показывающий, что количество таких циклов в ограниченной области может быть сколь угодно большим. Интенсивно занимается вопросами приложений дифференциальных уравнений в экономико-математическом моделировании. Станцо В.В. опубликовал 20 научных работ по теоретическим и прикладным вопросам теории дифференциальных уравнений.
Доцент Станцо Виталий Владимирович, кандидат физико–математических наук. Он является специалистом по качественной теории дифференциальных уравнений. Его исследования посвящены исследованию возникновения предельных циклов в трехпараметрических двумерных динамических системах. В частности, ему принадлежит результат, показывающий, что количество таких циклов в ограниченной области может быть сколь угодно большим. Интенсивно занимается вопросами приложений дифференциальных уравнений в экономико-математическом моделировании. Станцо В.В. опубликовал 20 научных работ по теоретическим и прикладным вопросам теории дифференциальных уравнений.
Доцент Зорина Ирина Григорьевна, кандидат физико – математических наук. Имеет более 10 научных публикаций по исследованию процессов теплообмена при фазовопереходных процессах в различных средах. Получены интересные результаты в теории подобия систем плазменной аэродинамики. Ее работы нашли практическое применение, в частности, при оптимизации ультразвуковых составных электроакустических преобразователей для обработки инфицированных ран.
 Доцент Покровский Леонид Дмитриевич, кандидат физико – математических наук. Высококвалифицированный специалист по задачам газовой динамики с нелинейной теплопроводностью, теории пограничного слоя. Его главные результаты относятся к области классификации и свойств решений уравнения переноса с нелинейностями общего вида (включая турбулентную фильтрацию).
Доцент Покровский Леонид Дмитриевич, кандидат физико – математических наук. Высококвалифицированный специалист по задачам газовой динамики с нелинейной теплопроводностью, теории пограничного слоя. Его главные результаты относятся к области классификации и свойств решений уравнения переноса с нелинейностями общего вида (включая турбулентную фильтрацию).
Леонид Дмитриевич в совершенстве владеет французским языком, что позволяет ему регулярно принимать участие в научных конференциях во Франции. Автор около 40 научных и методических работ. Он подготовил 3 кандидата физико – математических наук (среди них доцент кафедры Гласко А. В.).
 Доцент Копаев Анатолий Владимирович – кандидат физико – математических наук. Его научные интересы сосредоточены в области решения краевых задач теории аналитических функций (одной и нескольких переменных) и их применения в математической физике. Им предложен универсальный метод «функциональных уравнений» для решения задач сопряжения аналитических и гармонических функций, возникающих при описании установившихся фильтрационных течений несжимаемой жидкости в кусочно-однородных средах. Для решения одного из важнейших функциональных уравнений удалось построить интегро-дифференциальное преобразование, которое каждой гармонической в полупространстве функции трех переменных ставит в соответствие гармоническую в полуплоскости функцию двух переменных, зависящую от одного действительного параметра, а также найдено обратное преобразование. А.В. Копаевым опубликовано более 20 работ по данной тематике.
Доцент Копаев Анатолий Владимирович – кандидат физико – математических наук. Его научные интересы сосредоточены в области решения краевых задач теории аналитических функций (одной и нескольких переменных) и их применения в математической физике. Им предложен универсальный метод «функциональных уравнений» для решения задач сопряжения аналитических и гармонических функций, возникающих при описании установившихся фильтрационных течений несжимаемой жидкости в кусочно-однородных средах. Для решения одного из важнейших функциональных уравнений удалось построить интегро-дифференциальное преобразование, которое каждой гармонической в полупространстве функции трех переменных ставит в соответствие гармоническую в полуплоскости функцию двух переменных, зависящую от одного действительного параметра, а также найдено обратное преобразование. А.В. Копаевым опубликовано более 20 работ по данной тематике.
Доцент Аникин Анатолий Юрьевич, кандидат физико – математических наук, ведет исследования в области динамических систем классической механики. Основные направления его работы: гамильтонова динамика; хаос и интегрируемость в гамильтоновой динамике; локальные методы в гамильтоновой динамике; квазиклассический анализ; квантовая и статистическая механика с точки зрения классической. Им опубликованы три работы в зарубежных изданиях, в которых, в частности, доказан квантовый аналог теоремы Мозера о сходимости нормализующего преобразования для случая полутора степеней свободы; получен альтернативный язык, более алгебраический по сравнению со стандартным, для канонического формализма в неавтономном случае; получен квантовый аналог этого языка.
2. Теория вероятностей, математическая статистика, математическая теория надежности.
На кафедре сложился сильный коллектив специалистов, работающих в области теории вероятности и математической статистики, а также научных и технических приложений этих направлений. В частности, в области планирования, проведения и анализа результатов ускоренных испытаний, оценки надежности изделий в переменных режимах, а также прогнозирования показателей надежности сложных систем кафедра является одним из основных центров разработки новых идей и направлений.
 Профессор Белов Владимир Николаевич, доктор технических наук, автор 60 научных работ и 2 монографий. Является известным специалистом в области оценки показателей надежности сложных технических систем. Основное направление исследований: моделирование (скалярное, векторное) временных процессов различной природы.
Профессор Белов Владимир Николаевич, доктор технических наук, автор 60 научных работ и 2 монографий. Является известным специалистом в области оценки показателей надежности сложных технических систем. Основное направление исследований: моделирование (скалярное, векторное) временных процессов различной природы.
Полученные результаты:
- построены функционалы специального вида, позволяющие (при достаточно общих ограничениях на временной процесс) осуществлять пересчеты характеристик процесса от одних условий реализации к другим (статический, циклический, динамический режимы). Это позволило построить методы прогнозирования характеристик временного процесса в условиях (статических, циклических), требующих проведения длительных экспериментов, по результатам кратковременных испытаний (например, в динамических режимах);
- разработана процедура построения режима изменения внешних условий, обеспечивающего изменение требуемой характеристики процесса по заданной (но реализуемой) траектории;
- разработаны методы прогнозирования показателей надежности изделий радиоэлектроники в условиях эксплуатации по результатам лабораторных испытаний.
Частично результаты исследований представлены в двух монографиях:
- Белов В.Н. Детерминированные модели временных процессов. – Волгоград: Политехник, 2002;
- Белов В.Н. Стохастические модели временных процессов. – Волгоград: Политехник, 2002.
 Доцент Ветров Леонид Георгиевич, кандидат физико – математических наук. Являясь специалистом по теории вероятности (основные работы относятся к теории фильтрации мартингалов), он получил ряд интересных результатов в самых разнообразных прикладных областях. Им, в частности, исследовались вопросы построения системы бонус – малус в задачах автострахования; разработаны модели и методы проведения форсированных испытаний сложных систем и систем «без памяти»; получены модели поведения игроков на финансовом рынке валютных «фьючерсов». По этим направлениям им опубликовано более 40 научных публикаций в нашей стране и за рубежом.
Доцент Ветров Леонид Георгиевич, кандидат физико – математических наук. Являясь специалистом по теории вероятности (основные работы относятся к теории фильтрации мартингалов), он получил ряд интересных результатов в самых разнообразных прикладных областях. Им, в частности, исследовались вопросы построения системы бонус – малус в задачах автострахования; разработаны модели и методы проведения форсированных испытаний сложных систем и систем «без памяти»; получены модели поведения игроков на финансовом рынке валютных «фьючерсов». По этим направлениям им опубликовано более 40 научных публикаций в нашей стране и за рубежом.
 Профессор Калинкин Александр Владимирович, доктор физико-математических наук. Опубликовал около 60 научных работ по исследованию и моделированию стохастических систем с взаимодействием с марковскими процессами при дискретных состояниях.
Профессор Калинкин Александр Владимирович, доктор физико-математических наук. Опубликовал около 60 научных работ по исследованию и моделированию стохастических систем с взаимодействием с марковскими процессами при дискретных состояниях.
Разработанные им схемы взаимодействия широко используются для исследования вероятностных объектов физической кинетики, химической кинетики, экологии, в теории надежности технических систем (на рис. 2 представлены фазовая плоскость (а) и гистограмма (б)). Основные результаты:
- введены и классифицированы общие марковский процессы со взаимодействием при счетном множестве состояний на основе схемы взаимодействий;
- разработаны новые методы решения уравнений Колмогорова для производящих функций переходных вероятностей в нестационарном и стационарном случаях;
- для ряда процессов со взаимодействием выявлено нелинейное свойство (кинетическое уравнение) переходных вероятностей путем построения точных замкнутых решений первого и второго (линейных) уравнений Колмогорова.
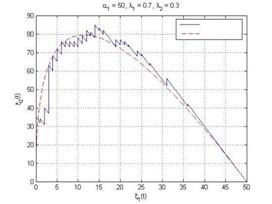
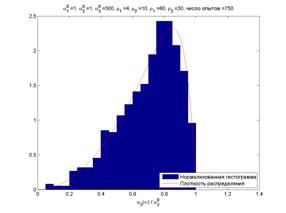
Полученные результаты: найдены решения первого и второго (линейных) уравнений Колмогорова для специальных классов марковских процессов: ветвящихся процессов, ветвящихся процессов с взаимодействием и других. Марковские процессы с взаимодействием определяются как модели эволюции систем частиц нескольких типов, согласно данной кинетической схеме. В случае независимости эволюций отдельных частиц друг от друга известно обыкновенное нелинейное дифференциальное уравнение для одночастичной производящей функции переходных вероятностей (кинетическое уравнение для одночастичной функции распределения). Фундаментальная проблема вывода третьего (нелинейного) уравнения теории марковских процессов разрешима через построение точных замкнутых решений линейных уравнений Колмогорова. Результаты исследований частично изложены в монографии “Markov’s branching processes with interaction”, Russian Mathematical Surveys, 2002, v. 57, p. 241-304.
 Профессор Павлов Игорь Валерианович, доктор физико-математических наук. Лауреат премии правительства РФ в области науки и техники за 2003 г. Видный специалист в области оценки и прогноза надежности больших технических систем на основе данных по испытаниям их компонент (элементов, подсистем). Его научные результаты отражены более чем в 60 научных трудах, а также в двух монографиях. Одним из основных направлений научной работы кафедры высшей математики (ФН -1) является математическая теория надежности и ряд связанных с ней направлений:
Профессор Павлов Игорь Валерианович, доктор физико-математических наук. Лауреат премии правительства РФ в области науки и техники за 2003 г. Видный специалист в области оценки и прогноза надежности больших технических систем на основе данных по испытаниям их компонент (элементов, подсистем). Его научные результаты отражены более чем в 60 научных трудах, а также в двух монографиях. Одним из основных направлений научной работы кафедры высшей математики (ФН -1) является математическая теория надежности и ряд связанных с ней направлений:
- Надежность и безопасность сложных технических систем, таких как современные системы энергетики, транспортные сети, системы радиоэлектроники, приборостроения и др.
- Испытания сложных технических систем
- Ускоренные испытания
- Оценка остаточного ресурса сложных технических систем
Математическая теория надежности как система соответствующих идей, математических моделей и методов оценки, прогноза и оптимизации показателей надежности, начала развиваться в послевоенные годы в связи с возрастающими требованиями к новой сложной технике. В 50-х годах вопросы надежности, испытания на надежность и задачи повышения надежности ракет и электронного оборудования стали привлекать значительное внимание, как математиков, так и инженеров – разработчиков новой техники. После чего в последующие годы появилось значительное число работ в этой области, в основном российских и американских ученых. При этом многие исследования шли параллельно и в некоторых вопросах удалось продвинуться дальше американским специалистам, а в некоторых – нашим. Основные работы сотрудников кафедры высшей математики МГТУ им. Н.Э.Баумана в области математической теории надежности и смежных областях.
Научные результаты:
- разработан метод определения наименьшего доверительного множества для вероятности безотказной работы сложной системы по аналогичным характеристикам ее компонент;
- получены оптимальные стратегии управления процессами замен и восстановления оборудования в сложных информационно – вычислительных комплексах;
- решена задача оптимального распределения вычислительных мощностей в системах с параллельными вычислительными модулями;
- исследованы оптимальные методы последовательной проверки сложных гипотез и доверительного оценивания функций многих неизвестных параметров.
Основные научные результаты отражены в монографиях:
- Павлов И.В. Статистические методы оценки надежности сложных систем. М.:Радиосвязь, 1982.;
- Гнеденко Б.В., Павлов И.В., Ушаков И.А. Статистическая теория надежности. Нью – Йорк, Wiley, 1999 г. (на англ. языке).
 Профессор Тимонин Владимир Иванович, доктор физико-математических наук, является автором около 40 научных работ в области непараметрической статистики, методов анализа результатов научных и технических экспериментов, а также применений этих методов в теории надежности, автострахования и медицины.
Профессор Тимонин Владимир Иванович, доктор физико-математических наук, является автором около 40 научных работ в области непараметрической статистики, методов анализа результатов научных и технических экспериментов, а также применений этих методов в теории надежности, автострахования и медицины.
Основные научные результаты Тимонина В.И. относятся к области исследования распределений классических статистик типа Колмогорова – Смирнова в двух – и многовыборочных вариантах, а также для полных и цензурированных выборок (статистики Реньи). К наиболее значительным результатам относятся:
- получен общий метод вычисления точных распределений любых статистик типа Колмогорова – Смирнова при справедливости степенных связей Кокса – Лемана между функциями распределения нескольких независимых выборок;
- впервые рассмотрена задача проверки степенных гипотез Кокса – Лемана в качестве основных и предложен критерий их проверки;
- для прогрессивно цензурированных выборок исследован критерий проверки их однородности и получены точные и асимптотические распределения его статистики, использующей оценки Каплана – Мейера функции выживания.
 Доцент Сунчалина Анна Леонидовна, кандидат физико – математических наук, ведет исследования в области оптимизации проведения форсированных испытаний. За счет использования параметрических двумерных моделей наработок до отказа изделий в разных режимах, основанных на ортогональном разложении плотностей, ей удалось существенно повысить точность определения корреляционных связей между этими наработками. Кроме того, ею существенно обобщены результаты Г.Д. Карташова в моделях форсированных испытаний сложных систем. Сунчалиной А. Л. опубликовано около 10 научных работ по этим направлениям.
Доцент Сунчалина Анна Леонидовна, кандидат физико – математических наук, ведет исследования в области оптимизации проведения форсированных испытаний. За счет использования параметрических двумерных моделей наработок до отказа изделий в разных режимах, основанных на ортогональном разложении плотностей, ей удалось существенно повысить точность определения корреляционных связей между этими наработками. Кроме того, ею существенно обобщены результаты Г.Д. Карташова в моделях форсированных испытаний сложных систем. Сунчалиной А. Л. опубликовано около 10 научных работ по этим направлениям.
3. Исследование операций
Работы в данном направлении ведутся как в теоретическом, так и прикладном направлениях.
Профессор Васильев Николай Семенович, доктор физико-математических наук, крупный специалист в области оптимального управления и численных методов, автор более 40 научных работ. Его основные результаты охватывают широкий спектр проблем:
- получены теоремы существования в минимаксных задачах и в дифференциальных играх;
- предложены методы поиска глобального экстремума в вогнутых задачах и поиска равновесий в n-матричных играх;
- исследованы модели глобальных сетей, для которых построены алгоритмы оптимальной маршрутизации сообщений на основе многокритериального подхода.
На основе полученных результатов предложены новые (многокритериальные и игровые) модели маршрутизации глобальных пакетных сетей, в которых осуществляется оптимизация быстродействия в условиях неопределенности и изменяющейся входной нагрузки. Разработан эффективный распределенный алгоритм управления маршрутами передачи, допускающий применение в режиме реального времени и обеспечивающий устойчивость потоков в сети. Проведенная серия вычислительных экспериментов с моделями глобальной сети Интернет, в частности с ее европейской частью, показала, что на этом пути может быть решена проблема эффективного обмена данными.

Профессор Грешилов А.А. – доктор технических наук, автор более 150 научных статей, 20 изобретений, 13 монографий. Он является одним из крупнейших российских специалистов по разработке и применению математических методов в анализе результатов научных экспериментов, имеющих важнейшее значение для страны. Основные направления его деятельности – ядерная физика (физика деления ядер), конфлюэнтный анализ, некорректные задачи, математические методы принятия решений.
Грешилов А.А. разработал оригинальные методы определения параметров ядерных взрывов по газообразным продуктам деления, а также параметров их нейтронного и гамма – излучений. Под его руководством создана подсистема перспективного планирования соответствующей отрасли. Математические модели конфлюэнтного анализа и методы оценки их параметров, автором которых является Грешилов А.А., стали теоретической основой разработки ряда спецпроектов.
Важное значение имеют разработанные им новые методы решения некорректных задач в многосигнальной радиопеленгации на одной частоте, позволяющие значительно повысить точность работы радиолокаторов. По этому направлению получено несколько авторских свидетельств.
Книги и монографии Грешилова А.А. как нельзя лучше отражают широчайший кругозор и глубину проработок решаемых им задач:
- Грешилов А.А. Некорректные задачи цифровой обработки информации и сигналов.- М.: Радио и связь, 1984.;
- Грешилов А.А. Прикладные задачи математического программирования. М.: Логос, 2006.;
- Ракетно-ядерное оружие и системы противоракетной обороны. Меч и щит России./ Коллектив авторов./ Калуга. Информационное агентство «Калуга-пресс», 2007.;
- Грешилов А.А., Егупов Н.Д., Матущенко А.М. Ядерный щит. – М.: Логос, 2008.
Профессор Смольяков Эдуард Римович – доктор физико – математических наук, автор около 200 научных работ, среди которых около 10 монографий. Смольяков Э.Р. является выдающимся специалистом в области теории игр и теории управления.
Смольяковым Э.Р. создана теория конфликтов, которую можно рассматривать как радикально новую теорию любых статистических и динамических игр. Эта теория предоставляет возможность получать решение, причем почти всегда единственное, любых конфликтных задач и игр – антагонистических, некооперативных, кооперативных и иных типов, как статических, так и динамических. Существенно, что эта теория дает единообразный подход к решению любых типов конфликтных задач, в отличие от классической теории игр, в которой задачи разных типов изучались независимо друг от друга и для которых не удавалось зачастую находить хотя бы какое – то решение.
На основе этой теории Смольяков Э.Р. построил математическую теорию быстрых межгалактических перелетов по каналам в магнитной вселенной, двойственной к нашей вселенной, а также разработать новое направление исследований, пограничное между математикой и физикой – экстремальную теорию размерностей, позволившую выводить точные дифференциальные уравнения любых процессов без использования физических законов и находить новые физические закономерности чисто математическим путем.
Во многом необычные и неожиданные результаты Смольякова Э.Р. изложены в ряде книг, в том числе:
- Смольяков Э.Р. Неизвестные страницы истории оптимального управления. М.:Едиториал УРСС, 2002;
- Смольяков Э.Р. Теория конфликтных равновесий. М.:Едиториал УРСС, 2005;
- Смольяков Э.Р. Теоретическое обоснование межзвездных перелетов. М.:КомКнига, 2005.
4. Функциональный анализ и алгебра

Профессор Исмагилов Раис Сальманович, доктор физико-математических наук. Один из блестящих математиков – теоретиков, имеющих глубокие результаты в самых абстрактных областях функционального анализа и алгебры. Опубликовано более 60 работ в изданиях, имеющих высший рейтинг как в России, так и за рубежом. Главные из результатов:
Спектральная теория операторов.
- изучены спектральные свойства классических операторов; получены результаты о спектре операторов Штурма-Лиувилля;
- построен аналог формулы Фейнмана-Каца для локально-компактных несвязных полей.
2. Представления групп.
- построены представления групп отображений многообразий в группы Ли, которые впоследствии были названы энергетическими;
- построены представления ряда классов бесконечномерных групп.
3. Теория приближений.
- решена одна из старейших классических задач о колмогоровских поперечниках функциональных классов; предложен метод усреднения в исследовании этих величин, оказавшийся весьма сильным средством исследования.
Результаты по теории представления групп опубликованы в монографии «Representations of infinite dimensional groups», AMS, v. 152.
Доцент Табалдыев Сейтек Болотбекович, кандидат физико – математических наук, – работает в области топологической гомологии – области функционального анализа, изучающей банаховы и локально выпуклые топологические алгебры и их непрерывные представления (банаховы и топологические модули) с использованием методов гомологической алгебры.
Главные научные результаты связаны с исследованием связи неприводимости, пространственной проективности операторной алгебры, нетривиальности её коммутанта и возможнвм наличием в этой алгебре столбца одномерных операторов. Табалдыевым С.Б. доказана неинъективность предуального бимодуля для алгебр мер на бесконечных дискретных группах. Учитывая, что алгебра мер на аменабельной группе аменабельна по Конну, тем самым отрицательно решён известный вопрос об инъективности предуального бимодуля для таких алгебр.
Результаты Табалдыева С.Б. опубликованы в 5 работах в ведущих российских и зарубежных журналах.

Доцент Храпов Павел Васильевич, кандидат физико – математических наук. Высококвалифицированный специалист в области функционального анализа, численных методов, методов оптимизации. Имеет более 30 научных публикаций. С 1986 является председателем студенческого научно-технического общества кафедры «Высшая математика» и председателем оргкомитета ежегодной студенческой научно-технической конференции кафедры «Весна». С 1988 член Московского Математического общества.
Основным направлением исследований является теория перколяции, модель Изинга в математической физике. Много занимался и прикладными вопросами статистического анализа – исследованию валютного рынка FOREX, разработкой методов анализа Data Mining (кластеризация, классификаторы, прогнозирование).
Доцент Огнева Ольга Семеновна, кандидат физико – математических наук. Основными направлениями ее исследований являются гомология топологических алгебр и анализ стохастических систем. Ее результаты нашли отражение в 10 научных работах, опубликованных в центральных изданиях.
5. Механика сплошной среды.
По этой тематике на кафедре работает ряд крупных специалистов, возглавляющие соответствующие направления в учреждениях АН РФ (МИ АН им. Стеклова, ВЦ АН РФ им. Дородницына и др.).

Профессор Ильичев Андрей Теймуразович, доктор физико-математических наук.
Его научные интересы сосредоточены в области теории распространения волн в диспергирующих средах, устойчивости локализованных волновых структур, исследовании поверхностей раздела в задачах гидромеханики, теории упругости и теории фильтрации. Он является автором свыше 30 научных работ. Главные результаты его работ приведены в монографии
Ильичев, А. Т. Уединенные волны в моделях гидромеханики. – М.: Физматлит, 2003. Профессор Ильичев А.Т. активно участвует в подготовке квалифицированных кадров преподавателей для кафедры. Его ученик, доцент кафедры Томашпольский В.Я., защитил диссертацию по тематике Андрея Теймуразовича, касающуюся распространения волн в упругих средах.
 Профессор Савин Александр Сергеевич, доктор физико-математических наук. Автор более 50 работ в задачах взаимодействия неоднородностей с границами раздела жидкостей с различными плотностями.
Профессор Савин Александр Сергеевич, доктор физико-математических наук. Автор более 50 работ в задачах взаимодействия неоднородностей с границами раздела жидкостей с различными плотностями.
Неоднородности различной природы, например, обтекаемые потоком преграды, источники массы, вихревые структуры и т.д., вызывают возмущения границ раздела сред. Расчет таких возмущений составляет содержание прямой задачи. В последнее время разработка систем мониторинга окружающей среды привела к необходимости восстановления физических полей в толще морской среды по данным зондирования границ раздела слоев с различными плотностями, в частности – свободной поверхности. При этом возникла гидродинамическая проблема: получить сведения о внутренней структуре потока по данным о его границах. Существенной частью этой общей проблемы является обратная задача генерации поверхностных и внутренних волн погруженными в поток неоднородностями.
Научные результаты:
- обобщен метод М.В.Келдыша на случай произвольного закона движения гидродинамических особенностей переменных интенсивностей;
- исследован характер установления поверхностных волн, генерируемых гидродинамическими особенностями;
- описано самоиндуцированное движение точечного вихря под свободной поверхностью жидкости;
- предложены различные подходы к задаче продолжения гидродинамических полей в толщу потока с его границы.
Результаты исследований частично изложены в монографии Савин А.С. Методы, процедуры и средства аэрокосмической компьютерной радиотомографии приповерхностных областей Земли. – М.: Научный мир, 1996.
 Профессор Шахов Евгений Михайлович, доктор физико-математических наук. Один из наиболее известных специалистов в области механики жидкости и газа. Основные и наиболее важные результаты получены в кинетической теории газов. По этой тематике им опубликовано около 120 работ. К главным результатам относятся:
Профессор Шахов Евгений Михайлович, доктор физико-математических наук. Один из наиболее известных специалистов в области механики жидкости и газа. Основные и наиболее важные результаты получены в кинетической теории газов. По этой тематике им опубликовано около 120 работ. К главным результатам относятся:
- - разработка метода аппроксимации канонического уравнения Больцмана;
- - новая кинетическая модель, или модель Шахова;
- - обобщение существующих численных конечно-разностных методов решения кинетических уравнений и решение на этой основе широкого спектра задач;
- - разработка способа определения локальных значений плотности и градиента плотности разреженной планетарной атмосферы по колебаниям легкого спутника-зонда, буксируемого орбитальным летательным аппаратом;
- - исследование основных закономерностей развития пространственных вихревых движений вязкой несжимаемой жидкости в полости тела, ускоренно вращающегося вокруг оси симметрии и/или около неподвижной точки (гироскопы с жидким наполнением).

Доцент Федотов Анатолий Александрович, кандидат физико – математических наук, автор около 30 научных работ.
Основные научные интересы: уравнения математической физики в механике сплошной среды, численные методы.
Главные научные результаты связаны с математическим моделированием работы машущего крыла в природе и технике:
- разработка математической модели крыла, работающего в режиме нормального трепещущего полета;
- разработка математической модели хвостового плавника дельфина, объясняющей происхождение оптимального способа плавания дельфина.
Федотов Анатолий Александрович – один из авторов патента РФ «Объемное голографическое антенное устройство».
 Доцент Бояринцева Татьяна Евгеньевна, кандидат физико – математических наук, автор более 10 научных работ. Ее исследования посвящены вопросам обнаружения различных вихревых структур в идеальной жидкости. Методы, развиваемые в ее работах, тесно связаны с задачами аэрокосмической компьютерной радиотомографии приповерхностных областей Земли. Руководит издательской деятельностью кафедры.
Доцент Бояринцева Татьяна Евгеньевна, кандидат физико – математических наук, автор более 10 научных работ. Ее исследования посвящены вопросам обнаружения различных вихревых структур в идеальной жидкости. Методы, развиваемые в ее работах, тесно связаны с задачами аэрокосмической компьютерной радиотомографии приповерхностных областей Земли. Руководит издательской деятельностью кафедры.
 Доцент Богомолов Владимир Георгиевич, кандидат физико – математических наук. Его работы посвящены вопросам взаимодействия оболочечных конструкций с жидкостью и динамике упругой оболочки в жидкости. Им опубликовано около 20 научных работ. Руководит методическим семинаром кафедры.
Доцент Богомолов Владимир Георгиевич, кандидат физико – математических наук. Его работы посвящены вопросам взаимодействия оболочечных конструкций с жидкостью и динамике упругой оболочки в жидкости. Им опубликовано около 20 научных работ. Руководит методическим семинаром кафедры.
 Доцент Янов Игорь Олегович, кандидат технических наук. Специализируется в области исследования динамики систем ориентации самолетов и космических аппаратов с использованием солнечного давления, а также идентификации параметров водопроводных сетей. В течение долгого времени работал по совместительству на кафедре ИУ-3 в должности старшего научного сотрудника. Является автором около 50 научных работ и 3 изобретений.
Доцент Янов Игорь Олегович, кандидат технических наук. Специализируется в области исследования динамики систем ориентации самолетов и космических аппаратов с использованием солнечного давления, а также идентификации параметров водопроводных сетей. В течение долгого времени работал по совместительству на кафедре ИУ-3 в должности старшего научного сотрудника. Является автором около 50 научных работ и 3 изобретений.
6. Теория атомарных и R – функций, вейвлеты, фракталы.
На кафедре работает один из создателей данного направления в современной математике.
 Профессор Кравченко Виктор Филиппович – заслуженный деятель науки РФ, доктор физико – математических наук, профессор, Главный научный сотрудник Института радиотехники и электроники РАН, главный редактор и основатель международного журнала «Электромагнитные волны и электронные системы», а также «Успехи современной радиоэлектроники», автор более 650 научных работ, в числе которых 20 монографий и 11 авторских свидетельств. В.Ф. Кравченко – основатель научной школы: под его руководством защищено 10 докторских и 17 кандидатских диссертаций. Один из ведущих в мире специалистов в новейших областях современной математики – теории атомарных и R – функций, вейвлетов, фракталов. Его научные достижения находят широкое применение на практике: в цифровой обработке сигналов и изображений, в краевых задачах математической физики. Он участвовал в многочисленных международных симпозиумах и конференциях.
Профессор Кравченко Виктор Филиппович – заслуженный деятель науки РФ, доктор физико – математических наук, профессор, Главный научный сотрудник Института радиотехники и электроники РАН, главный редактор и основатель международного журнала «Электромагнитные волны и электронные системы», а также «Успехи современной радиоэлектроники», автор более 650 научных работ, в числе которых 20 монографий и 11 авторских свидетельств. В.Ф. Кравченко – основатель научной школы: под его руководством защищено 10 докторских и 17 кандидатских диссертаций. Один из ведущих в мире специалистов в новейших областях современной математики – теории атомарных и R – функций, вейвлетов, фракталов. Его научные достижения находят широкое применение на практике: в цифровой обработке сигналов и изображений, в краевых задачах математической физики. Он участвовал в многочисленных международных симпозиумах и конференциях.
Основные научные результаты следующие:
- решены на основе теории R – функций для областей сложной формы краевые задачи электродинамики, теплопроводности, акустики; исследованы проблемы, связанные с построением координатных последовательностей для основных вариационных и проекционных методов, краевых условий различных типов и областей сложной формы;
- решены с помощью нового типа эквивалентных граничных условий (задачи третьего рода) внутренние и внешние краевые задачи электродинамики сверхпроводящих структур:
- разработана теория сверхпроводящих резонаторов, позволившая получить эффективные алгоритмы по уточнению фундаментальной физической константы скорости света;
- разработана на основе атомарных функций (АФ) теория цифровой обработки сигналов;
- созданы новые классы весовых функций и новый класс WA – систем функций Кравченко – Рвачева;
- на основе АФ исследованы обобщенные ряды Котельникова и полиномы Левитана;
- решены задачи анализа и синтеза антенн на основе АФ;
- разработан новый класс атомарно-фрактальных функций и создана теория фрактальных антенных решеток;
- исследованы физические модели электродинамических и тепловых полей, позволившие решить задачи радиолокационного и радиотеплового картографирования подстилающих поверхностей различной природы с помощью космических аппаратов.
Кравченко В.Ф. – главный редактор журналов «Электромагнитные волны и электронные системы», «Успехи современной радиоэлектроники».
Основные научные издания Кравченко В.Ф.за последние годы:
- В.Ф. Кравченко Лекции по теории атомарных функций и некоторым их приложениям. М.: Радиотехника, 2003.
- В.Ф. Кравченко, В.Л. Рвачев Алгебра логики, атомарные функции и вейвлеты в физических приложениях. М. Физматлит, 2006.
- В.К. Волосюк, В.Ф. Кравченко Статистическая теория радиотехнических систем дистанционного зондирования и радиолокации. Под ред. В.Ф. Кравченко М.: Физматлит, 2008.
- В.А. Дорошенко, В.Ф. Кравченко. Дифракция электромагнитных волн на незамкнутых поверхностях. Под ред. В.Ф. Кравченко. М.: Физматлит, 2009.
- В.Ф. Кравченко, О.С. Лабунько, А.М. Лерер, Г.П. Синявский. Вычислительные методы в современной радиофизике. Под ред. В.Ф. Кравченко. М.: Физматлит, 2009.
Современные исследования кафедры высшая математика
В настоящее время исследования проводятся с целью получения фундаментальных научных результатов мирового уровня одновременно в нескольких классических областях математики, а также происходит формирование и развитие новых областей математики и их приложений.
Работа проводиться одновременно в нескольких направлениях под руководством ведущих специалистов в соответствующих областях, докторов наук, представителей ведущих научных школ. В каждом направлении решаться целый круг задач. Так например:
- Спектральная теория сигналов на основе атомарных и R-функций; теория ортогональных рядов, построенных на основе атомарных функций; атомарные и R-функции в теории вероятностей и случайных процессов; новый класс двумерных WA-систем функций Кравченко-Рвачева в цифровой обработке сигналов и изображений; алгоритмы и методы для использования атомарных и R-функций в задачах цифровой обработки сигналов и изображений, краевых задач математической физики, теории вероятностей и случайных процессов, квантовой механики и электродинамики; программы ЭВМ для расчета необходимых параметров физических моделей; математическое обеспечение на основе программ ЭВМ.
- Усложнённые равновесия для игровых задач, подход к разрешению проблемы единственности решения игровых задач, два сильных равновесия для игровых задач, расширенная система взаимно связанных конфликтных равновесий, конфликтно устойчивые Парето-подобные равновесия.
- Использование особых экстремалей для получения новых уравнений движения и неизвестных констант, методы вывода уравнений экстремальной динамики и универсальные уравнения свободного движения, теория вывода дифференциальных уравнений произвольных процессов, методы поиска дифференциальных уравнений произвольных динамических процессов, принцип движения без инерциальных перегрузок с остановкой «внутреннего» времени.
- Изучение спектральных инвариантов преобразований и их места в динамике. Развитие методов определения статистических свойств динамических систем; динамических свойств преобразований; алгебраических свойств преобразований; спектральной функции кратности для естественных факторов декартовых произведений перемешивающих преобразований, косых произведений динамических систем, хорошо аппроксимированных преобразований; топологического статуса различных динамических свойств. Изучение спектральных инвариантов типичных групповых действий. Исследования подпространств с тривиализующимися типичными динамическими системами. Модели пространств динамических систем, действующих на рациональных пространствах Урысона путем выбора удобной меры и пространств динамических систем, действующих на расширениях Канторовых множеств. Изучение преобразований на спектре динамических систем. Классификация инвариантных мер: вокруг гипотезы Фюрстенберга.
- Исследование возмущения спектра дифференциальных операторов Штурма-Лиувилля, Шредингера и их векторных аналогов в зависимости от изменения потенциала. Исследование зависимости колмогоровских поперечников компактов от вложения данного метрического пространства в линейное нормированное пространство, изучение операторов Рака для групп движений евклидова пространства и других классов локально-компактных групп, изучение представлений групп, связанных с математическим анализом и математической физикой (групп гладких преобразований, групп функций со значениями в данной группе Ли).
- Краевые задачи для эллиптических операторов с переменными коэффициентами в ограниченных и неограниченных областях, обобщенный критерий Вейля и принцип Бирмана локализации спектра, энергетический метод оценки резольвенты вблизи непрерывного спектра, энергетический метод доказательства непрерывности спектра. Критерий Реллиха дискретности спектра, методы теории весовых пространств С.Л. Соболева, гильбертов метод единственности получения точной управляемости в задачах граничного управления.
- Модель обтекания профиля крыла в системе крыла дозвуковым и трансзвуковым потоком и значения аэродинамических коэффициентов, решение обратных задач аэродинамики для определения профиля по заданным распределениям нагрузки или скорости потока по его поверхности, расчет пограничного слоя в условиях ламинарно-турбулентного обтекания с вычислением точки перехода, модель обтекания профилей с усложненными свойствами, проницаемости поверхности, расчет аэродинамических характеристик крыла при внесении конструктивных изменений и вариациях положения элементов компоновки, оптимизация профилировки крыла.
- Модель геотермальной системы как с резкой поверхностью фазового перехода, так и с зоной смеси при переходе пар-жидкость (так называемые «тепловые трубы»). Исследование устойчивости поверхности/зоны фазового перехода. Модель артерии, как нелинейной упругой осесимметричной мембраны, наполненной жидкостью. Исследованное нелинейных локализованных гидро-упругих волн в рамках данной модели, исследование устойчивости аневризмы (стоячей локализованной волны).
- Модель взаимодействия процессов восприятия элементарных внешних стимулов, модель процесса восприятия музыкальной мелодии, программы ЭВМ, реализующие эти модели, основы теории Г-последовательностей, математическое определение сознания и подсознания (сознательного и бессознательного), обобщение модели динамики внимания в процессе восприятия элементарного внешнего стимула на произвольные психические процессы (воспоминания, воображения, мышления и пр.), новая физиологическая интерпретация внимания. Поисковая работа по приложению конвергентного уравнения диффузии для построения моделей других систем (ориентировочно: урбанизация, формирование монополий, рост муравейников, фазовые переходы 1-го рода, самосборка наноструктур).
- Оценка показателей надежности, ресурса и остаточного ресурса сложных технических систем. Оценка и прогноз характеристик прочности изделий. Модели для оценки прочности изделий по результатам статистических испытаний на прочность их фрагментов. Оптимальные стратегии управления процессами замен и восстановления оборудования в сложных информационно – вычислительных комплексах большой мощности, обеспечивающие заданные гарантированные характеристики надежности и эффективности функционирования таких систем. Оптимальное распределение вычислительных мощностей в таких системах.
- Уравнения математической физики, функциональный анализ, качественная и спектральная теория дифференциальных уравнений, спектральная теория операторов, абстрактная теория приближений, теория групп и теория представлений, эргодическая теория и динамические системы, теория чисел, кодирование, дескриптивная теория множеств, топология, теория вероятностей и случайных процессов. Марковские цепи, теория надежности, цифровая обработка сигналов и изображений, статистическая теория распознавания образов, квантовая теория, аэрокосмические технологии, транспортные системы, использование тепловой энергии геотермальных резервуаров, диагностика и лечение сосудистых заболеваний и дальнейшее изучение тока крови в сосудах, теория ресурсов внимания.
Области применения научной продукции: математика, физика, техника, психология, физиология, медицина, экономика, военное дело.
Результаты НИР востребованы следующими организациями:
ИРЭ им. В.А. Котельникова РАН, НТЦ УП РАН, ФГУП НИИ «Прецизионного приборостроения», ОАО НПК НИИ Дальней радиосвязи, ОАО «Концерн радиостроения «Вега»», Радиочастотный центр Южного Федерального округа, институт психологии РАН, НИИ высшей нервной деятельности им. И.П. Павлова.
Результаты НИР внедряются в образовательный процесс в виде курсов лекций в МГТУ им. Н.Э. Баумана и МГУ им. М.В. Ломоносова студентам, обучающимся по соответствующим специальностям. В частности, могут быть включены в специальные курсы: «Атомарные функции, вейвлеты и фракталы в физических приложениях», «Теория конфликтов и дифференциальные игры», «Обобщенное оптимальное, стохастическое и конфликтное равновесия», «Уравнения математической физики», «Одномерный оператор Шредингера», «Основы математической теории надежности», «Испытания технических систем», «Теория оптимальных статистических решений», «Обобщенные функции и линейные операторы». Также в процессе выполнения НИР могут быть созданы новые специальные курсы по тематике НИР.
Основные характеристики НИР
За последние 10 лет профессором Э.Р. Смольяковым была создана теория конфликтов, которую, в частности, можно рассматривать как радикально новую теорию любых статических и динамических игр. Эта теория предоставляет возможность получать решение, причём почти всегда единственное, любых конфликтных задач и игр – антагонистических, некооперативных, кооперативных и иных типов, как статических, так и динамических. С практической точки зрения существенно, что эта теория даёт единообразный подход к решению любых типов конфликтных задач, в отличие от классической теории игр, в которой задачи разных типов изучались независимо друг от друга и зачастую для них не удавалось найти не только единственное, но и хотя бы какое-нибудь удовлетворительное решение.
На основе этой теории автору в последние несколько лет удалось, в частности, построить математическую теорию быстрых межгалактических перелётов по каналам в магнитной вселенной, двойственной к нашей вселенной, и разработать новое направление исследований, пограничное между математикой и физикой – экстремальную теорию размерностей, позволившую выводить точные дифференциальные уравнения любых процессов без использования физических законов и находить новые физические закономерности и фундаментальные физические постоянные чисто математически путём.
В рамках намеченных исследований планируется продолжить работу по фундаментальным проблемам математики, теоретической физики, теории конфликтов и игр и теории оптимального управления, а также разработать основы совершенно новой области исследований – экстремальной теории размерностей, впервые сформулированной автором в 2008 г.
В настоящее время исследования проводятся в следующих направлениях:
- Разработка новых понятий конфликтного равновесия, которые в совокупности с ранее найденными автором понятиями конфликтного равновесия позволили бы получать единственное решение любых конфликтных и игровых задач – антагонистических, некооперативных и кооперативных, как статических, так и динамических.
- Создание математически обоснованной экстремальной теории размерностей – совершенно новое научной направление, лежащее на стыке математики и теоретической физики, начальные основы которого были впервые заложены автором в 2008 г.
- С помощью экстремальной теории размерностей получение новых фундаментальных физических постоянных, параметров подобия и уравнения, открывающие новые горизонты исследований в физике, технике и экономике.
- Поиск общих уравнений свободного движения произвольных физических объектов и процессов, реализующие движение в пространстве при управляемом «внутреннем» течении времени, причём не испытывая инерциальных перегрузок.
По данной тематике предполагается опубликовать порядка 10 статей в центральных академических журналах, в частности, в журналах «Доклады АН РФ», «Дифференциальные уравнения», «Кибернетика и системный анализ», «Автоматика и телемеханика», «Динамика неоднородных систем».
В настоящее время рассмотрены классические дифференциальные операторы (операторы Штурма-Лиувилля, Шредингера, а также векторные аналоги этих операторов), ограничиваясь операторами с дискретным спектром. Основная задача заключается в исследовании возмущения спектра в зависимости от изменения потенциала. Имеющаяся к настоящему времени теория позволяет оценить это возмущение спектра при условии достаточной регулярности потенциалов и их возмущений. В случае произвольных возмущений картина оказывается достаточно сложной. Она будет предметом будущих исследований.
Аппроксимативные характеристики метрических пространств были предметом многочисленных исследований последних десятилетий. Важнейшая из этих характеристик – это Колмогоровские поперечники компактов, лежащих в линейных нормированных пространствах. В частности, представляет интерес зависимость этих величин от вложения данного метрического пространства в линейное нормированное пространство. Имеющиеся к настоящему времени предварительные результаты показывают, что эта тема допускает достаточно интересное развитие.
В последнее время профессором Р.С. Исмагиловым было предложено обобщение понятия коэффициентов Рака, известного в теории представлений полупростых групп Ли и в квантовой механике, на общие локально – компактные группы. Это привело к понятию операторов Рака для представлений групп данного класса. При исследовании этих операторов обнаружились содержательные связи этой темы с вопросами геометрии и теории специальных функций. В процессе выполнения НИР будет проведено изучение указанных операторов для групп движений евклидова пространства. Кроме того, будут продолжены исследования операторов Рака для других классов локально-компактных групп.
Будет продолжено изучение представлений групп, связанных с математическим анализом и математической физикой (групп гладких преобразований, групп функций со значениями в данной группе Ли). Эти представления рассматривались Р.С. Исмагиловым в его книге «Representations of infinite dimensional groups, AMS, 1996.» В частности, речь идёт о представлениях в пространствах обобщённых функций, об условиях их унитарности в соответствующих подпространствах и других вопросах, характерных для теории представлений.
Математическое моделирование в механике сплошных сред
Проблемы взаимодействия газовых сред с обтекаемыми телами на протяжении многих лет являлись предметом исследований. В последние десятилетия эти исследования были сосредоточены в основном на двух направлениях. Первое связано с математическим моделированием до – и трансзвукового обтекания крыловых профилей, второе – с научными разработками в области фундаментальных проблем сверхзвуковых и гиперзвуковых течений газа. В рамках первого направления предполагается изучить следующие проблемы: обтекание профиля крыла в системе крыла дозвуковым и трансзвуковым потоком и вычисление аэродинамических коэффициентов; решение обратных задач аэродинамики для определения профиля по заданным распределениям нагрузки или скорости потока по его поверхности; расчет пограничного слоя в условиях ламинарно-турбулентного обтекания с вычислением точки перехода; обтекание профилей с усложненными свойствами, проницаемости поверхности; расчет аэродинамических характеристик крыла при внесении конструктивных изменений и вариациях положения элементов компоновки; оптимизация профилировки крыла.
В области фундаментальных проблем высокоскоростных течений газа значительное внимание будет уделено вопросам совершенствования формы быстро летящих тел с целью достижения оптимальных значений аэродинамических характеристик при различных совокупностях изопериметрических условий.
В середине 70-х годов стало ясно, что при сверхзвуковых скоростях только переход от тела вращения к эквивалентному телу с некруговым миделевым сечением может привести к значительному снижению аэродинамического сопротивления. Начало этому направлению было положено в работах Г.Г.Черного, А.Л.Гонора и других авторов. Результатом этих исследований явился новый объект – тела с сублимирующим покрытием. Однако имевшиеся знания, базировавшиеся на ряде точных решений, результатах решения вариационных задач и отдельных экспериментах, не позволяли давать рекомендации по использованию летательных аппаратов подобной конструкции.
В связи с этим предполагается проведение в широких теоретических и экспериментальных исследованиях сверх- и гиперзвукового обтекания пространственных тел, включающих изучение структуры возмущенного течения, свойств аэродинамических характеристик при различных режимах полета и наборах геометрических параметров и создание на этой основе достаточно простых и эффективных моделей расчета, позволяющих с достаточной точностью получать оценки аэродинамического сопротивления указанных тел и проводить их оптимизацию.
Теоретически в рамках модели идеальной жидкости и с использованием различных методов, в том числе – специального оптического метода, изучаются иначе невидимые течения. В частности, теоретически обнаружены и получили экспериментальное подтверждение топологически новые структуры конических линий тока с особенностями в ударном слое при наличии маховской конфигурации ударных волн. Показано, что при их реализации нагрузка на угловую конфигурацию в окрестности режимов обтекания с плоскими ударными волнами, лежащими в плоскости передних кромок и принадлежащими на передних кромках к сильному семейству, терпит разрыв. Построены новые типы ветвления ударных волн в конических течениях с висячими скачками уплотнения, обнаруженные в эксперименте. Обнаружены режимы автоколебаний, обусловленные отрывом пограничного слоя.
В результате исследований установлена фундаментальная общность свойств отрыва турбулентного пограничного слоя в конических и плоских потоках. Построены эмпирические соотношения, позволяющие определять положение и размер области отрыва турбулентного пограничного слоя для широкого круга типов взаимодействия конических ударных волн и систем скачков уплотнения с пограничным слоем, а также прогнозировать глобальную перестройку структуры течения в конических угловых конфигурациях. Эти результаты значительно опережают соответствующие зарубежные исследования. Определена роль каждого из параметров геометрии в снижении сопротивления различных тел по сравнению с эквивалентными телами вращения. Определена область изменения параметров, где конические тела с сублимирующим покрытием обладают значительно меньшим полным сопротивлением по сравнению с эквивалентными конусами и оптимальными степенными телами вращения.
Решение проблемы устойчивости полета пространственных тел с учетом известных способов стабилизации потребовало изучения ряда фундаментальных вопросов: о положении центра давления пространственных тел и его зависимости от условий полета; о возможности создания компоновок, обладающих запасом статической устойчивости без использования дополнительных стабилизирующих устройств, значительно снижающих преимущество в сопротивлении по сравнению с эквивалентными телами вращения; об аэродинамике оптимальных пространственных форм при их стабилизации вращением.
Впервые поставлена задача о форме конических тел в сверхзвуковом потоке, положение центра давления которых не зависит от числа Маха и угла атаки. Предполагается определение точных и приближенных решений, представляющие практический интерес. Построение теории конических тел, обладающих максимальным запасом статической устойчивости при различных изопериметрических условиях. Подтверждение результатов теории, в том числе обнаруженного закона подобия, что позволяет рекомендовать найденные пространственные конфигурации в качестве формы устойчивого сверхзвукового летательного аппарата с малым сопротивлением и высокими несущими свойствами, обеспечивающими быстрое затухание колебаний тела около центра масс. Построение теории оптимальных пространственных тел минимального волнового сопротивления, вращающихся в гиперзвуковом потоке.
Результаты, полученные в рамках гиперзвуковой теории идеального газа, нельзя считать окончательными. Кроме исследований, связанных с выбором оптимальных форм аппаратов, летящих с большой скоростью, будет выполнен цикл работ по сверхзвуковому обтеканию источников тепловыделения, а также развита линейная теория обтекания крыловых профилей запыленным газом, изучено обтекание затупленных тел газовзвесью в широком диапазоне скоростей набегающего потока. С использованием аналитических и численных методов будут выявлены новые физические эффекты взаимодействия газа с источником энерговыделения, сформулированы новые принципы формирования сверхзвуковых потоков с нужными для приложений свойствами, проведены расчеты влияния энергоподвода на аэродинамические характеристики быстро летящих тел. Учет присутствия дисперсных частиц в газовых потоках позволил выявить новые качественные закономерности течений двухфазных сред. В частности, отмечено, что при обтекании крылового профиля наличие дисперсной примеси способно приводить к возникновению значительных дестабилизирующих аэродинамических моментов, которые при определенных условиях действуют в сторону уменьшения угла атаки. Предполагается исследовать возможность эффективного управления параметрами теплообмена с помощью двухфазного вдува на обтекаемой поверхности. Предполагается предложить новый лагранжев метод расчета течений сред, описываемых уравнениями континиума без собственных напряжений. Метод основан на привлечении дополнительных уравнений для компонент якобиана перехода от эйлеровых к лагранжевым переменным, тем самым позволяя рассчитывать все параметры среды (включая плотность) из решения обыкновенных дифференциальных уравнений на фиксированных траекториях.
Исследования по механике вязких жидкостей и газовой динамики будут развиваются, главным образом, по трем направлениям: пограничный слой, гидродинамическая неустойчивость и переход к турбулентности, развитие и приложение численных методов к решению уравнений Навье-Стокса, Эйлера, Прандтля. Развитие их предполагает создание новых научных школ по гидродинамической устойчивости. Что касается численных решений задач вязкой жидкости, то исследования в этом направлении будут связаны с идеей об особой эффективности прямых методов Галеркина в комбинации с конечноразностными процедурами. Один из таких подходов, известный как метод Галеркина-Петрова, оказался особенно полезным не только для решения линейных задач устойчивости, но и для анализа нелинейных колебательных и волновых процессов в течениях вязкой жидкости.
Исследования будут направлены на изучение фундаментальных свойств вязких потоков, таких, как неустойчивость и переход к турбулентности, вихреобразование и перенос завихренности при обтекании тел конечных размеров, отрывы и автоколебания в зонах отрыва, образование и динамика поверхностей раздела и свободных поверхностей в вязких потоках, перестройки потока под воздействием внешних объемных и поверхностных сил. Выбор конкретных задач определялся актуальными запросами современной технологии, экологии, техники. Значительная часть проводимых исследований будет посвящена течениям со свободными поверхностями и с поверхностями раздела, в частности, капиллярным течениям в струях при различной геометрии удерживающих и формирующих поток твердых поверхностей.
Большой интерес представляют изучение свойств нелинейных, и особенно, сильно нелинейных волн в вязкой жидкости в условиях, когда они развиваются под воздействием капиллярных сил, силы тяжести и внешних воздействий. Исследование их с применением прямых методов приводит к нелинейным математическим моделям с диссипацией и дисперсией. Объект исследования составляют пограничные слои, ограниченные свободными поверхностями, и пограничные слои вблизи поверхностей раздела. Возможность применения приближения пограничного слоя к таким течениям была установлена уже в первых работах по динамике капиллярных пленок, поверхностей раздела. Эффективность этого подхода была отчетливо продемонстрирована истолкованием экспериментов П.Л.Капицы и С.П.Капицы по волнообразованию в стекающих пленках еще в 1967 г. К настоящему времени получила законченное оформление концепция пограничного слоя с самоиндуцированным давлением, которое возникает при деформациях свободной поверхности от воздействия капиллярных сил. Для адекватного описания движений свободной поверхности с большой амплитудой, например, сильно нелинейных волн, разработан способ соответствующего обобщения уравнений Прандтля. Такие исследования включают: решение уравнений Навье-Стокса в приближении пограничного слоя для течений тонких слоев со свободными границами и границами раздела, исследование гидродинамической неустойчивости стационарных и нестационарных пленочных течений, анализ нелинейного развития возмущений в пленках и формирование волн, струек, капель. Предполагается установить ряд закономерностей фундаментального характера. Роль вязкости, формирующей профиль скорости в слое, оказывается существенной, т.к. может приводить к появлению профильной неустойчивости, отличной от неустойчивости Релея и Кельвина-Гельмгольца.
Новое развитие получила задача о пограничном слое на поверхности раздела, развивающемся под воздействием трения на поверхности. В многочисленных экспериментах установлено, что касательная сила возникает при изменениях поверхностного натяжения, вызванных вариациями температуры или концентрации примесей. Проведенные расчеты спектров неустойчивости таких пограничных слоев открыли новые моды неустойчивости и наметили направление исследований для истолкования сложной картины турбулизации поверхности. Процессы гидродинамической неустойчивости, порождающие волновые структуры на поверхности, развиваются при сравнительно небольших числах Рейнольдса. Это обстоятельство позволяет успешно применять прямые методы для изучения динамики волновых эффектов жидкости. Содержательная нелинейная модель течения построена осреднением по толщине жидкого слоя системы уравнений Навье-Стокса.
Исследования по теории нелинейных волн направлено на решение модельных уравнений. Разработанные методы найдут эффективное приложение к изучению неустойчивости и нелинейных волн, усложненных процессами тепло – и массообмена. Анализ проблем обобщения и приложений модельных уравнений показал, что часто применяемые слабонелинейные модельные уравнения являются частными случаями модельных уравнений при стремлении к нулю единственного свободного параметра подобия, отражающего условия экспериментов. Как следствие этого, нелинейные волновые решения предельных модельных уравнений представляют лишь математические волны.
Изучены численные методы динамики вязкой жидкости. В связи с нелинейностью основных уравнений численные методы играют существенную роль в аэрогидродинамике. Они применяются не только для доведения до конечного численного результата решений отдельных задач, но, главным образом, для выявления фундаментальных свойств течений. Особенно это относится к течениям вязкой жидкости. По сложившейся традиции развитие численных методов аэромеханики и газовой динамики ориентировано на применение прямых методов при гибком комбинировании их с методами конечных разностей. Численные методы решения линейных и нелинейных проблем гидродинамической устойчивости предполагается разрабатывать для изучения неустойчивости, нелинейного развития возмущений и переходов к сложным пространственным структурам в потоках с границами раздела и зонами отрыва, формирующихся в закрученных потоках и при обтекании плоских тел вязкой жидкостью. Исследованы критические значения параметров, при которых происходит потеря устойчивости стационарных течений, изучается нелинейный переход к новым периодическим или квазипериодическим состояниям и находятся решения уравнений Навье-Стокса для вторичных течений. В частности, предполагается решить проблему отыскания собственных чисел для системы уравнений Орра-Зоммерфельда. Это создает возможность находить области неустойчивости и наиболее растущие возмущения в двухслойных капиллярных течениях, управляемых свободными параметрами.
Проведены численные эксперименты по надежному моделированию ламинарного и турбулентного закрученного течения с застойной зоной ламинарным потоком с эффективным числом Рейнольдса, которому соответствует подходящее решение уравнений Навье-Стокса. Проведены исследования взаимодействий неустойчивостей и зон отрыва при обтекании профиля крыла с перфорированной и непроницаемой поверхностью дозвуковым и трансзвуковым потоком газа. Усовершенствованы вычислительная схема для расчета базовой задачи об обтекании сложного тела, сопровождаемым формированием нестационарной зоны отрыва с вихревой дорожкой. Отработаны алгоритмы, программы и постановки задач, учитывающих развитие неустойчивости в пограничном слое от носика профиля до зон отрыва.
Моделирование и изучение геотермальных систем проведены в рамках законов теории фильтрации: закона сохранения массы, импульса (закона Дарси), энергии и фазового равновесия в зонах смеси с соответствующими условиями на границах и поверхностях фазового перехода. Для изучения устойчивости течений в геотермальных системах использованы достоверные методы теории гидродинамической устойчивости. Для моделирования сосудов (артерий и вен) использованы методы нелинейной теории оболочек, теории мембран и теории идеальной жидкости. Для исследования устойчивости нелинейных локализованных волн в сосудах использованы методы теории функций комплексного переменного (построение функции Эванса), методы теории гамильтоновых систем и численные методы для нахождения решений конечной амплитуды, подлежащих исследованию на устойчивость.
Получены стационарные решения уравнений движения в геотермальных системах с поверхностью фазового перехода. Это решение соответствует вертикальному потоку с движениями фаз. Давления в фазах распределены линейно по высоте, а температуры – экспоненциально. Положение поверхности фазового перехода определяется из граничных условий на данной поверхности и удовлетворяет трансцендентному уравнению. Предполагается предпринять анализ этого уравнения, как аналитический, так и численный.
Получено стационарное решение, отвечающее стационарному вертикальному потоку в слое смеси в пористой среде. На нижней границе «тепловой трубы» задано давление и насыщенность, а на верхней – давление. Стационарное решение не выписывается в явном виде, в связи со сложной структурой нелинейных уравнений, описывающих подобные течения. Будет предпринят асимптотический анализ соответствующего решения и исследованы различные асимптотики.
Методом нормальных мод предполагается получить дисперсионное уравнение в модели течений в геотермальной системе с поверхностью фазового перехода линеаризацией основных уравнений модели вокруг вертикального стационарного течения. В дисперсионное уравнение должно входить много физических параметров системы, что затрудняет его анализ. Предполагается проанализировать дисперсионное соотношение в зависимости, в первую очередь от проницаемости, и построить критические диаграммы устойчивости при меняющейся проницаемости и фиксированных других параметров системы. Ожидается, что присутствуют два типа перехода к неустойчивости: через нулевое волновое число и через бесконечное волновое число (при меняющейся проницаемости).
Для анализа устойчивости солитонных решений основных уравнений течения жидкости в сосудах имеется одна объективная трудность – точное решение типа уединенной волны неизвестно, хотя доказано его существование и получено приближение в пределе малой амплитуды. Форма уединенной волны, соответствующей точному солитонному решению полной системы уравнений, может быть определена только численно. В связи с этим задача об устойчивости уединенной волны может быть решена только при помощи комбинации аналитических и численных методов. На первом этапе предполагается численно определить диапазон скоростей спектрально неустойчивых уединенных волн.
Дальнейшие исследования включают в себя линеаризацию основных уравнений вокруг солитонного решения, построение функции Эванса и доказательство того факта, что функция Эванса аналитична в окрестности нуля и на положительной вещественной полуоси в плоскости спектрального параметра, сравнение поведения функции Эванса в окрестности нуля и на бесконечности в плоскости спектрального параметра (при помощи численных методов).
Для того чтобы установить диапазон скоростей, в котором уединенная волна устойчива, потребуется гамильтонова формулировка основных уравнений с последующим анализом.
Будет разработан метод исследования устойчивости вертикальных стационарных течений в «тепловых трубах». Задача сводится к построению неустойчивых глобальных мод неоднородного обыкновенного дифференциального уравнения, полученного линеаризацией основных уравнений вокруг стационарного решения. Численно будут получены вторичные структуры конечной амплитуды за порогом неустойчивости в задаче с твердыми границами, между которыми находится слой смеси в пористой среде. Ожидается, что вторичные структуры будут носить ярко выраженный конвективный характер и иметь ячеистый тип, как в задаче Релея-Бенара о тепловой конвекции.
В рамках НИР кафедры решаются также следующие задачи.
Оценка показателей надежности и ресурса сложных технических систем (системы энергетики, информационно-вычислительные и телекоммуникационные системы, и др.) на основе статистических данных по их испытаниям.
Оценка и прогноз характеристик прочности изделий на основе стохастических моделей полумарковских процессов, связывающих основные макро – характеристики прочности с их локальными нано – характеристиками. Построение соответствующих моделей для оценки прочности изделий по результатам статистических испытаний на прочность их фрагментов.
Построение оптимальных стратегий управления процессами замен и восстановления оборудования в сложных информационно – вычислительных комплексах большой мощности (с параллельными вычислительными модулями), обеспечивающих заданные гарантированные характеристики надежности и эффективности функционирования таких систем. Оптимальное распределение вычислительных мощностей в таких системах.
Профессором Кравченко В.Ф. развита теория R-функций (функций В.Л. Рвачева), атомарных функций и вейвлетов. Получен алгебрологический метод R-функций. Рассмотрено его применение к расчетам физико-механических полей различной природы. Построен новый класс W-систем функций Кравченко-Рвачева и исследовано его применение к задачам обнаружения кратковременных знакопеременных и сверхширокополосных процессов. Результаты исследований используются в современных методах вычислительной математики и ее приложениями, а также при решении краевых задач различной физической природы, цифровой обработки сигналов и изображений. Основы теории R-функций (1963 г.) были заложены В.Л. Рвачевым в оригинальной работе «Об аналитическом описании некоторых геометрических объектов», опубликованной в ДАН СССР (т. 153, №4, с. 765 – 768) и представленной академиком А.А. Дородницыным. Одним из основных результатов, полученных на основе теории R-функций (функций В.Л. Рвачева), является решение обратной задачи аналитической геометрии. В. Л. Рвачев разработал и обосновал математическую теорию R-функций, а также практические ее приложения в следующих областях науки и техники: оптимальное размещение геометрических объектов, распознавание образов, математическое программирование, конструктивная теория функций и особенно решение краевых задач математической физики различной физической природы. В течение длительного времени применение классических вариационных методов сдерживалось отсутствием конструктивных математических средств для построения в явном виде координатных функций, точно удовлетворяющих заданным краевым условиям для областей сложной формы и обладающих свойствами полноты. Профессором Кравченко В.Ф. с помощью конструктивного аппарата теории R-функций (функций В.Л. Рвачева) разработан и обоснован единый подход к проблеме построения координатных последовательностей вариационных и проекционных методов не только задачи Дирихле или Неймана, но и краевые условия самых различных типов для областей произвольной формы. Это позволило с помощью теории R-функций (RFM) добиться больших успехов при решении важных прикладных задач теории упругости, изгиба и колебаний тонких пластин, теплопроводности, дифракции упругих волн, электродинамики. Впервые получен целый ряд новых результатов: обобщены ряды В.А. Котельникова на основе АФ, рассмотрена теория Стренга-Фикса и обобщенная теорема отсчетов, а также полиномы Левитана с помощью АФ, R-функции и соотношение неопределенности для пространственных сигналов, локализованных в области сложной формы, системы функции с двойной ортогональностью и обобщенное соотношение неопределенности, учет ограничений на искомый сигнал с применением R-функций, впервые рассмотрено применение распределения Вигнера-Вилля в сочетании с АФ к цифровой обработке сигналов (ЦОС). В связи с активным развитием цифровых систем обработки информации в последнее время стали актуальными вопросы разработки алгоритмов ЦОС в радиолокационных станциях (РЛС), основанные на современных вычислительных методах. Одним из таких является современный вейвлет-анализ.
Так как свойства вейвлет функций во многом схожи со свойствами сверхширокополосных сигналов (СШП), то нашли широкое применение методы обнаружения кратковременных знакопеременных и сверхширокополосных процессов в различных радиофизических приложениях. Кроме известных вейвлет-систем (И. Добеши, И.Мейера, Стронберга-Лемарье-Бэтли, Хаара, В-сплайны Шенберга и др.), проведено построение и обоснование нового класса WA-систем функций Кравченко-Рвачева на основе АФ.
Ингрид Добеши (автор известной книги «Десять лекций по вейвлетам») пишет: «Вейвлеты появились в 80-х годах 20 века как альтернатива оконного преобразования Фурье для анализа сигналов. Вскоре стало очевидно, что они представляют собой намного больше, являясь по сути, реинкарнацией идей, которые уже существовали ранее во множестве других областей. Подобная участь постигает многие новые идеи. В случае с вейвлетами круг различных областей, с которыми они, как выяснилось, связаны, отличается удивительной широтой и охватывает помимо всего прочего, жесткие оценки в чистой математике, понятии групп, ренормализации в физике, субполосную фильтрацию в электротехнике и схемы последовательного деления в области вычислительной техники. Представляя более чем просто синтез идей из многих различных областей, вейвлеты добавили новые грани к каждой из них, дав ключ к новому пониманию и упростив старые подходы.»
Следует заметить, что теория АФ появилась в оригинальных работах В.Л. и В.А. Рвачевых примерно на восемь лет раньше, чем вейвлеты И. Добеши и других зарубежных специалистов. Показано, что новый класс вейвлетов Кравченко-Рвачева представляют собой СШП сигналы, поэтому разложение СШП сигналов по этим вейвлетам является естественным и обоснованным. Вейвлет-спектр СШП сигналов, преобразованный на основе вейвлетов Кравченко-Рвачева, имеет хорошую локализованность. Это обусловлено тем, что имеется сходство физических параметров исследуемых СШП сигналов с базисными функциями вейвлет-преобразования. Новый класс вейвлет-функций может быть использован не только в задачах обнаружения сигналов на фоне слабо коррелированных помех, определения местоположения источника СШП сигнала, измерения информационных параметров СШП сигналов, но и в краевых задачах математической физики при решении интегральных уравнений первого или второго рода.
Учебно-методическая работа
Кафедра ведет общематематическую подготовку на четырех факультетах: «Машиностроительные технологии», «Робототехника и комплексная автоматизация», «Инженерный бизнес и менеджмент», «Фундаментальные науки», а также на кафедре «Юриспруденция». Заместителем заведующего кафедрой по учебной работе является доц. Вилисова Н. Т.
Для студентов факультета МТ кафедра ведет следующие дисциплины: математический анализ, аналитическая геометрия, линейная алгебра, теория поля, теория функций комплексного переменного. Для студентов старших курсов преподаватели кафедры разработали специальные курсы:
Для специальностей МТ-1, МТ-2, МТ-3, МТ-4, МТ-6, МТ-8, МТ-10, МТ-11 теория вероятностей и математическая статистика (доц. Богомолов В. Г., доц. Вилисова Н. Т., доц. Покровский Л. Д., проф. Сидняев Н. И., проф. Шахов Е. М., доц. Янов И. О.).
Для специальности МТ-2 уравнения математической физики и метод конечных элементов (доц. Федотов А. А.).
Для специальности МТ-4 теория принятия статистических решений и программные статистические комплексы (проф. Павлов И. В., доц. Ветров Л. Г.).
Для специальностей МТ-5 и МТ-7 уравнения математической физики и элементы вариационного исчисления (проф. Филиновский А. В., доц. Федотов А. А.).
Для специальностей МТ-8 и МТ-10 уравнения математической физики (проф. Белов В. Н., доц. Янов И. О.).
Для специальности МТ-12 методы математической физики и вычислительной математики (доц. Храпов П.В.).
Для специальности МТ-13 математические методы и модели исследования надежности и ресурса (проф. Павлов И. В.).
Заведует секцией МТ ст. преп. Мастихин А. В.
Для студентов факультета РК кафедра ведет общие курсы, а также спецкурсы:
Для специальности РК-4 теория вероятностей, уравнения математической физики и дискретная математика (проф. Калинкин А. В., проф. Смольяков Э. Р., доц. Бояринцева Т. Е.).
Для специальности РК-5 вариационное исчисление, тензоры и уравнения математической физики (доц. Паршев Л. П.), функциональный анализ (доц. Храпов П. В.).
Для специальности РК-6 математическая логика и теория алгоритмов, дискретная математика (проф. Исмагилов Р. С., доц. Бояринцева Т. Е., ст. преп. Золотова Н. В.), вычислительная математика (доц. Храпов П. В.).
Для специальностей РК-9 и РК-10 теория вероятностей и математическая статистика, методы оптимизации и дискретная математика (проф. Калинкин А. В., проф. Смольяков Э. Р.).
В течение многих лет секцией РК заведовала ст. преп. Ефрюшкина В.А. В настоящее время секцией РК заведует доц. Томашпольский В. Я.
Для студентов факультета ИБМ кафедра ведет общие курсы, а также спецкурсы: теория вероятностей и математическая статистика, исследование операций (проф. Васильев Н. С., проф. Грешилов А. А., проф. Исмагилов Р. С., доц. Станцо В. В.,доц. Сунчалина А. Л.).
Заведует секцией ИБМ ст. преп. Воробьева Е. А.
Организация учебно-методической работы на кафедре «Высшая математика» во многом определяется принятым учебным планом, указывающим направление и содержание подготовки высококвалифицированных специалистов.
За многие годы на кафедре высшая математика сложилась и оправдала себя следующая организационная структура учебно-методической работы. На кафедре создана методическая комиссия, имеющая рекомендательные функции. Поле деятельности методической комиссии обширно: она организует, направляет и контролирует методическую работу кафедры, принимает рекомендательные решения по постановке отдельных учебных дисциплин, их взаимной увязке с другими общими и профилирующими дисциплинами, рассматривает внедрение технических средств в учебный процесс, новых форм и методов обучения и многое другое.

Методическую работу на кафедре возглавляет опытный специалист доцент, к.ф.-м.н., Сергей Константинович Соболев. Автор ряда блестящих учебников и учебно-методических пособий. Наиболее популярные из них:
1. Сборник задач по линейной алгебре. М, МГТУ им. Баумана. 1991. г.
2. Пособие для поступающих в вузы в 6 частях. МГТУ им. Н.Э. Баумана, 1996-1997 гг.
3. Исследование и построение плоских кривых, заданных параметрически и в полярных координатах. М, МГТУ. 2005.
4. Геометрия для 10-11 кл. Электронный учебник (на двух дисках), – М. Кирилл и Мефодий,– 2006.
5. Криволинейные интегралы. Электронное издание, М. – 2008.
6. Векторная алгебра. Электронное издание. М, МГТУ им. Н.Э. Баумана.
Корректировка и составление новых учебных планов по всем специальностям факультетов обязательно проводится с участием методической комиссии. Каждый учебный план должен получить одобрение комиссии, в противном случае он не будет представлен на утверждение в деканат. То же касается и учебных программ по всем дисциплинам (как общим, так и профилирующим), читаемым на факультете.

Методическая комиссия на кафедре ФН-1 «Высшая математика» – это штаб по выработке всех материалов, обеспечивающих учебный процесс:
– программы дисциплин (а их на кафедре более 60);
– календарные планы всех этих дисциплин (в этих планах содержание дисциплин расписано по лекциям и упражнениям, по каждой лекции приведена рекомендованная литература, а по каждому занятию указан перечень задач для решения, как в аудитории, так и дома);
– пакеты всех контрольных работ и аттестаций по этим дисциплинам, индивидуальных домашних заданий, вопросы и билеты к экзаменам и зачетам;

– все методические пособия в бумажном и электронном виде, специально написанные для студентов МГТУ им. Н.Э. Баумана и значительно облегчающие им овладение математическими дисциплинами с первого по шестой курсы;
– критерии оценки всех видов учебной деятельности студентов, как в течение семестра, так и на экзамене или зачете.
От хорошей и правильно организованной учебно-методической работы в большей степени зависит правильная реализация учебного плана, а, следовательно, и конечная цель — подготовка специалистов, имеющих глубокие и прочные знания, умеющих самостоятельно приобретать их как в вузе, так и на производстве.
Уровень учебно-методической работы определяется, прежде всего, квалификацией преподавателя, его методическим опытом и, конечно, постановкой этой работы на кафедре, как основном звене организации учебно-методической работы в Университете. Кафедра «Высшая математика» уделяет большое внимание учебно-методической работе. В соответствии с учебным планом силами штатных преподавателей, а также высококвалифицированных специалистов, приглашаемых из академических институтов, проводятся все виды учебных занятий (лекции, практические и лабораторные занятия, курсовое и дипломное проектирование, производственные практики и т. п.).
Важно определить виды учебной работы, которые должны выполнять преподаватели кафедры в зависимости от их квалификации. Совершенно очевидно, что такие виды учебных занятий, как чтение лекций, руководство дипломным и курсовым проектированием, которые требуют высокой квалификации и большого методического опыта преподавания, необходимо поручать только профессорам и доцентам.  В течение многих лет в Училище установлено, что профессор — заведующий кафедрой помимо основной учебной нагрузки должен в год читать лекции объемом не менее 100—120 ч, профессор кафедры — не менее 120—150 ч, ибо лекция была и остается основным видом учебного процесса в вузе. На кафедре в конце текущего учебного года, имея учебный план (учебный отрезок) на следующий учебный год, на заседаниях определяют и утверждают для каждого преподавателя в зависимости от его квалификации и занимаемой должности виды учебной нагрузки и их объем в часах, которые затем вносятся в его индивидуальный план работы. Последний подписывается заведующим кафедрой и утверждается деканом факультета. Два раза в течение учебного года (после каждого семестра) преподаватели на заседаниях кафедры отчитываются о выполнении индивидуальных планов работы. Сводный отчет по каждой кафедре сдается в Учебно-методическое управление, контролирующее эту работу. В зависимости от профиля кафедры виды учебных занятий и их объем (в часах) для преподавателей, занимающих одни и те же должности, будут разные. Чтение лекций и проведение других видов занятий проходит в строгом соответствии с учебными программами, что в значительной степени определяет полное и рациональное выполнение учебного плана по каждой дисциплине и позволяет должным образом организовать и контролировать учебно-методическую работу преподавателей кафедры. Особенно это важно при изучении базовых дисциплин по высшей математике, которые в основном изучаются студентами на первых трех курсах. Контроль за выполнением учебной программы преподавателями осуществляют заведующий или заместитель заведующего кафедрой по учебной работе или по указанию заведующего — ведущие преподаватели кафедры (например, руководители секций по факультетам на общенаучных и общеинженерных кафедрах). Наиболее оправдавшими себя формами контроля являются посещение и обсуждение содержания всех видов учебных занятий и методик их проведения на заседании кафедры или ее секции.
В течение многих лет в Училище установлено, что профессор — заведующий кафедрой помимо основной учебной нагрузки должен в год читать лекции объемом не менее 100—120 ч, профессор кафедры — не менее 120—150 ч, ибо лекция была и остается основным видом учебного процесса в вузе. На кафедре в конце текущего учебного года, имея учебный план (учебный отрезок) на следующий учебный год, на заседаниях определяют и утверждают для каждого преподавателя в зависимости от его квалификации и занимаемой должности виды учебной нагрузки и их объем в часах, которые затем вносятся в его индивидуальный план работы. Последний подписывается заведующим кафедрой и утверждается деканом факультета. Два раза в течение учебного года (после каждого семестра) преподаватели на заседаниях кафедры отчитываются о выполнении индивидуальных планов работы. Сводный отчет по каждой кафедре сдается в Учебно-методическое управление, контролирующее эту работу. В зависимости от профиля кафедры виды учебных занятий и их объем (в часах) для преподавателей, занимающих одни и те же должности, будут разные. Чтение лекций и проведение других видов занятий проходит в строгом соответствии с учебными программами, что в значительной степени определяет полное и рациональное выполнение учебного плана по каждой дисциплине и позволяет должным образом организовать и контролировать учебно-методическую работу преподавателей кафедры. Особенно это важно при изучении базовых дисциплин по высшей математике, которые в основном изучаются студентами на первых трех курсах. Контроль за выполнением учебной программы преподавателями осуществляют заведующий или заместитель заведующего кафедрой по учебной работе или по указанию заведующего — ведущие преподаватели кафедры (например, руководители секций по факультетам на общенаучных и общеинженерных кафедрах). Наиболее оправдавшими себя формами контроля являются посещение и обсуждение содержания всех видов учебных занятий и методик их проведения на заседании кафедры или ее секции.
 Кафедры стремятся добиваться стабильности учебных программ дисциплин, но вместе с этим при неизменных учебных планах систематически проводить необходимую и методически оправданную их корректировку. Такое отношение к учебным программам позволяет методически правильно, на глубокой научной основе преподавать учебные дисциплины, организует и дисциплинирует работу преподавателей и студентов. Кроме того, стабильность учебных программ в значительной степени облегчает согласование дисциплин между собой как по содержанию, так и по времени их изложения и устраняет дублирование учебного материала. Последнее еще важно и потому, что учебный план в настоящее время очень напряжен по содержанию и ограничен по времени.
Кафедры стремятся добиваться стабильности учебных программ дисциплин, но вместе с этим при неизменных учебных планах систематически проводить необходимую и методически оправданную их корректировку. Такое отношение к учебным программам позволяет методически правильно, на глубокой научной основе преподавать учебные дисциплины, организует и дисциплинирует работу преподавателей и студентов. Кроме того, стабильность учебных программ в значительной степени облегчает согласование дисциплин между собой как по содержанию, так и по времени их изложения и устраняет дублирование учебного материала. Последнее еще важно и потому, что учебный план в настоящее время очень напряжен по содержанию и ограничен по времени.
Стремясь как можно более полно и эффективно использовать каждый час учебных занятий, кафедра высшая математика проводит постоянную целеустремленную работу по устранению описательного и второстепенного материала из лекций, вынося их на самостоятельную проработку студентами. Такая работа, прежде всего, важна для профилирующих кафедр, так как прямым образом связана с усилением и улучшением теоретического уровня преподаваемых учебных дисциплин. На заседаниях ученых советов регулярно слушаются вопросы, касающиеся повышения теоретического уровня различных циклов подготовки студентов и учебных дисциплин в отдельности. Как известно, глубина и прочность получаемых студентами знаний зависят от многих факторов, главным из которых является хорошо поставленная и организованная, четко планируемая и постоянно контролируемая методическая работа каждого преподавателя. Нельзя совершенствовать учебный процесс и добиваться хороших знаний студентов, не улучшая методическую работу, не придавая ей первостепенного значения. Методическая работа, связанная с совершенствованием учебного процесса, представляет собой большой перечень мероприятий. В число их входят: методически правильное чтение лекций и проведение других видов занятий с учетом имеющихся учебников, учебных пособий и технических средств обучения; написание учебников, учебных пособий и методических пособий для дисциплин, по которым нет учебников; методически обоснованное включение в учебные дисциплины результатов выполненных НИР на кафедре и использование научного оборудования для лабораторных работ студентов; разработка и создание необходимых схем, а также интернет-семинаров для широкого использования аудиовизуальных средств; определение содержания и объема (как в количественном, так и в качественном отношении) всех видов самостоятельной работы студентов, прежде всего домашних заданий и расчетных работ; оборудование учебных аудиторий, позволяющих правильно проводить учебные занятия.
Как отмечалось, основным звеном в проведении учебно-методической работы в Университете является кафедра. Кафедра высшей математики конкретизирует учебно-методическую работу с учетом специфики специальностей, имеющихся на факультетах. С этой целью организованы секции по факультетскому принципу. Секция является первичным звеном организации учебно-методической работы. Возглавляют секции ведущие преподаватели кафедры. На кафедре стремятся к тому, чтобы каждый преподаватель работал только в одной секции и обслуживал специальности только одного факультета, причем долгие годы. Такая организация секций позволяет каждому преподавателю кафедры познать необходимую специфику факультетов, установить постоянную и деловую связь с деканатами и профилирующими кафедрами факультетов. В целом же за постановку учебно-методической работы на кафедре несет ответственность заведующий кафедрой.
Коллектив кафедры систематически совершенствует учебный процесс на научной основе, разрабатывает научный подход к определению содержания, организационных форм и методов обучения, а также проводит воспитательную работу со студентами.
На кафедре выработаны единые взгляды и накоплен большой опыт. Научная организация учебного процесса представляет собой комплекс мероприятий, направленных на дальнейшее совершенствование сложившейся на кафедре системы подготовки инженеров широкого профиля для машиностроительной и приборостроительной промышленности. Наиболее важными из них являются:
- проведение научно-методической работы по правильному отбору и передаче информации;
- рациональное использование бюджета времени студентов и преподавателей на основе систематического его изучения;
- развитие высокой степени самостоятельности и активности студентов в освоении дисциплин учебного плана;
- широкое применение в учебном процессе современных технических средств обучения и особенно вычислительной техники;
- совершенствование планирования и организации учебного процесса;
В настоящее время на заседаниях часто поднимается вопрос о том, чему и как учить в математике. Постановка его связана с повышением роли математических методов как при решении конкретных практически важных задач, так и при проведении самых разнообразных теоретических исследований. Необходимо отметить, что одной из ведущих тенденций современного развития науки и техники является все более интенсивное использование математических методов для анализа закономерностей окружающего мира, как с количественной стороны, так и с качественной. Особенно возросла роль математики в связи с широким внедрением современных вычислительных систем (суперкомпьютеров, кластеров и т.д.) во все сферы человеческой деятельности. Это обусловливает необходимость повышения требований к математической подготовке специалистов-математиков так и не математиков.
Математизация является характерной чертой современной науки и техники. Человечество ныне, как никогда, осознало, что знание делается точным только тогда, когда для его описания удается использовать математическую модель (либо уже известную, либо специально созданную). Эту роль и значение математики хорошо понимал еще Галилей. Он писал: «Философия написана в грандиозной книге— Вселенной, которая открыта нашему пристальному взгляду. Но понять эту книгу может лишь тот, кто научился понимать ее язык и знаки, которыми она изложена. Написана же она на языке математики…». Вместе с увеличением объема приложений математики продолжает интенсивно развиваться, и она сама, причем ее развитие, как и всегда, стимулируется не только внешними, но и внутренними факторами.
В настоящее время в результате появления суперкомпьютеров появились качественно новые возможности использования математических методов. Они применяются ныне не только там, где это делалось издавна (например, в механике, физике, астрономии), но и там, где несколько десятков лет назад об этом почти не было речи (в экономике, геологии, социологии, лингвистике, биологии, медицине, управлении и т. д.). Важно отметить, что с появлением новых возможностей использования математики, связанных с современной вычислительной техникой, не потеряли своего значения и методы классической математики, в частности качественные математические исследования. С помощью подобных методов производится, например, правильная постановка математических задач, нужных для практики, создание новых математических моделей, отбор материала для проведения вычислений на ЭВМ и разработка новых вычислительных методов. Современная математика представляет собой стройную и глубокую совокупность знаний о математических моделях со своими проблемами, с собственными путями развития, обусловленными внешними и внутренними причинами и задачами. Математика представляет интерес, прежде всего сама по себе как совокупность объективных истин. Кроме того, математика дает удобные и плодотворные способы описания самых разнообразных явлений реального мира и тем самым выполняет в этом смысле функцию языка. Наконец, и это очень важно, математика дает специалистам мощные методы исследования как теоретических, так и чисто практических проблем. С помощью математики решается много важных и актуальных технических и экономических задач, имеющих первостепенное значение для хозяйства страны, что превратило математику в производительную силу общества.
Физико-математические дисциплины составляют научную базу, на которой в высшей школе строится общеинженерная и специальная подготовка будущих специалистов.
При обучении математике, прежде всего, встают основные вопросы: «Чему надо учить по математике в университете? На что обращать основное внимание? Как учить, т. е. на каких основных принципах должна базироваться методика обучения математики? Какие изменения необходимо внести в программы по математике, чтобы в них нашло свое отражение современное развитие математических методов, нужных для решения практических задач»? При этом следует исходить из того, что время, отведенное на изучение математики в высших учебных заведениях, не может быть сколько-нибудь существенно увеличено по сравнению с тем, которое на нее уже отведено, хотя определенное увеличение здесь безусловно необходимо. Основой, на которой надо базироваться при решении этих принципиальных задач, должен являться в первую очередь уровень подготовки специалистов, требуемый для успешной работы в тех или иных областях современной науки или техники. Нельзя, конечно, не учитывать и перспективные пути их развития и не принимать во внимание ожидаемые потребности ближайшего и более отдаленного будущего. Характерной чертой работы специалиста сегодняшнего дня является работа в быстро меняющихся ситуациях, требующих новых подходов. Поэтому помимо определенного запаса знаний образование должно дать умение ориентироваться в меняющейся обстановке. А выработать такое умение нельзя, обучая только применению готовых рецептов (чему, тем не менее, необходимо продолжать учить). Надо учить пониманию основных принципов данной науки, свободному владению ее основными понятиями, методами, в частности методами математического моделирования, причем (и это очень важно) не только детерминированного, но и вероятностного. Следует помнить, что результат обучения оценивается не количеством сообщенной информации, а качеством ее усвоения, умением ее применять и развитием способностей обучаемого к дальнейшему самостоятельному образованию. Все это относится как к чистой, так и к прикладной математике, в том числе и к обучению использованию вычислительной техники. Необходимость широкой и достаточно глубокой подготовки современных специалистов приводит к сближению высшего технического и университетского образования и созданию своеобразных технических университетов, ярким примером которых является МГТУ им. Н.Э. Баумана. За последние годы в преподавании математики в высших технических учебных заведениях заметны довольно существенные изменения, оказывающие благотворное влияние на математическое образование специалистов. Математическими кафедрами МГТУ им. Н.Э. Баумана проделана значительная работа по углублению содержания курса математики, усилению его прикладной направленности, внедрению в преподавание вероятностно-статистических, численных методов, а также по совершенствованию методики преподавания с использованием компьютерных средств и программированного обучения.
Курс математики приобрел большую, чем раньше, прикладную направленность. Студенты обучаются использованию современной вычислительной техники и программных комплексов для численного решения задач. В программу обучения включены необходимые для этого разделы теории, например элементы теории разностных схем, элементы математической логики, исследования операций и т. д. Обучение численным методам, как правило, основывается на фундаментальном общематематическом образовании. Происходит синтез анализа и линейной алгебры, значительно усилилась роль теории вероятности и математической статистики, что нашло свое отражение в выделении на них большего числа часов в общем курсе математики, чем это было прежде. Вообще, следует отметить повышение общего уровня преподавания математики.
Вместе с тем наряду с достигнутыми положительными результатами имеется и ряд нерешенных серьезных проблем. Так, например, многое предстоит сделать по внедрению вычислительной техники в учебный процесс, по совершенствованию методов преподавания, по внедрению математических методов в специальную подготовку студентов, по привитию студентам навыков самостоятельной работы. Необходимо внедрить новые учебные программы, включить в них современные разделы прикладной математики. Основной задачей для преподавателей кафедр высшей математики сейчас является усиление фундаментальной математической подготовки студентов при ее прикладной направленности. Чтобы успешно решить эту задачу, надо ясно отдавать себе отчет в том, что цель обучения математики — это приобретение студентами определенного круга знаний, умения использовать изученные математические методы, развитие математической интуиции и математической культуры, необходимой для чтения специальной литературы и для продолжения в случае необходимости математического образования, что преподавание математики должно быть по возможности простым, ясным, естественным и базироваться на уровне разумной строгости, что на первых этапах обучения надо отдавать предпочтение индуктивному методу, постепенно подготавливая и используя дедуктивный подход.
При этом надо помнить, что нельзя научить приложениям математики и решению задач на ЭВМ математическими методами, не научив самой математике, и что нельзя овладеть самой математикой, не владея ее основами. Следует отметить опасность замены математических понятий в процессе обучения их конкретными реализациями. Математика изучает соотношения между элементами: математических моделей, количественные и качественные связи между ними. С помощью математических моделей можно и следует изучать конкретные явления, для которых они служат математическими моделями, но это уже приложения математики, а не сама математика. Нередко математическая модель смешивается с реальным явлением, для описания которого она в каком-то смысле пригодна. Это иногда приводит к искажению целей преподавания математики и порождает весьма спорные высказывания о методе обучения математике лиц, использующих ее для решения прикладных задач. Смысл математического понятия не зависит от области его дальнейшего применения. Математика едина. Нет чистой и прикладной математики, есть математика и ее приложения. Обычно прикладной математикой называется применение качественных и количественных математических методов к изучению какой-либо конкретной практической задачи, в частности численное решение подобной задачи. Подобные вопросы не являются изолированной частью математики, а неразрывно связаны с ее чисто теоретическими и качественными исследованиями. Поэтому деление математики на чистую и прикладную искусственно и не может быть четко определено. Поскольку математика едина, то, в частности, так называемую чистую математику и численные методы следует изучать как единое целое, иллюстрируя ее применение на решении тех или иных конкретных задач.
Очень важными являются философско-идеологические основы курса математики. Именно с самого начала при изучении теоретических основ следует идеологически готовить студента к численному решению задач как к следующей, в ряде случаев более сложной ступени изучения математических моделей и вместе с тем прививать ему практические навыки обращения с современной вычислительной техникой. Прежде всего, при обучении математике целесообразно обращать внимание на характер доказательств рассматриваемых теорем, отмечая, когда он является алгоритмическим, а когда нет. Полезно, также заметить, что не всякий алгоритмический процесс на самом деле целесообразно использовать на практике, что большое значение для применения алгоритма в счисленных расчетах имеет число операций, которые надо совершить при его использовании, и объем памяти, которую при этом надо иметь. Весьма целесообразно параллельно с рассмотрением основных понятий математического анализа обучать сразу студентов численному решению задач, иллюстрирующих изучаемые понятия и их свойства. Итак, усиление прикладной направленности математического образования в МГТУ им. Н.Э. Баумана следует понимать как дальнейшее изучение прикладных методов в процессе всего обучения студента на базе прочного фундамента основных математических знаний.
Правильное решение поставленной основной задачи об усилении фундаментальной математической подготовки при ее практической направленности должно касаться улучшения изучения математики на всех уровнях. Очень важным здесь является наличие непрерывного математического образования студента во все время пребывания его в МГТУ им. Н.Э. Баумана. Математическое образование студента не должно кончаться изучением курса общей математики, курсом программирования и использования вычислительной техники, оно должно продолжаться и при изучении специальных дисциплин.
Кафедра высшей математики нацелена:
- участвовать в выполнении комплексных исследований по профилю ПНР университета совместно со специальными кафедрами;
- принимать участие вместе со специальными кафедрами в руководстве студенческими научными, курсовыми и дипломными работами студентов;
- разрабатывать планы непрерывной математической подготовки студентов и активно содействовать их реализации;
- практиковать составление совместно с другими кафедрами единых планов использования современных компьютеров на весь период обучения;
- организовать постоянно действующие семинары для преподавателей других кафедр и аспирантов по изучению методов современной прикладной математики.
Выше уже говорилось о том, что современному инженеру приходится работать в быстро меняющихся ситуациях. Сказанное в полной мере относится и к преподавателям высших учебных заведений. Не секрет, что многие из преподающих математику, из числа получивших классическое математическое образование, имеют весьма отдаленное представление о современной вычислительной технике и ее применении. Поэтому следует обратить особое внимание на методы повышения квалификации преподавателей, в частности на работу факультетов, занимающихся этим вопросом. На заседании кафедры остро поставлен вопрос о необходимости обучения методам современной математики преподавателей. В современных условиях роль математических кафедр не может быть ограничена лишь общенаучной подготовкой студентов. Кафедры математики призваны оказывать самое непосредственное влияние на содержание и уровень специальной подготовки будущих инженеров. Повышению этого уровня способствовало бы использование спецкурсов математики, входящих в состав новой программы, разработанной на кафедре «Высшая математика». Было бы заблуждением думать, что улучшения в математическом образовании можно добиться лишь за счет изменения программ. Очень важным и принципиальным вопросом является методика преподавания, не нужно жалеть время и силы на ее совершенствование. Важным фактором является и чувство ответственности преподавателя за свою работу. Учить надо тому, что нужно и чему трудно научиться. При этом преподаватель обязан не только, учить, но и научить студента.
Хорошее усвоение математики немыслимо без интенсивных самостоятельных занятий студентов. Вопросам организации самостоятельной работы уделяется значительное внимание на заседаниях. Для развития у студентов навыков самостоятельной работы, особенно у студентов младших курсов, кафедра организует четкую систему контроля за самостоятельной работой путем проведения регулярного оперативного контроля, выдачи индивидуализированных заданий для лабораторных и расчетных работ, проведения теоретических аттестаций и контрольных работ по разделам (темам), выдачи курсовых работ для всех студентов на кафедрах с повышенной математической подготовкой и для наиболее способных студентов в остальных кафедрах. Наиболее сильные студенты привлекаются к участию в конкурсах и олимпиадах по математике.
Подготовка специалистов на факультете ФН
В 1999 году кафедра «Высшая математика» стала выпускающей. Она осуществляет подготовку инженеров-математиков по специальности «прикладная математика», специализирующихся в области стохастического анализа и моделей обработки информационных массивов.
Для студентов факультета ФН преподаватели кафедры разработали специальные курсы, некоторые из которых являются уникальными:
- Основы математической теории надежности, теория оптимальных статистических решений, испытание технических систем (проф. Павлов И.В.)
- Статистический анализ данных по цензурированным выборкам, многомерный статистический анализ (проф. Тимонин В. И.)
- Марковские модели систем с взаимодействием (проф. Калинкин А.В.)
- Методы выборочного обследования (доц. Ветров Л. Г.)
- Вейвлеты и атомарные функции цифровой обработки сигнала (проф. Кравченко В. Ф.)
- Теория массового обслуживания (проф. Белов В. Н.)
- Теория планирования эксперимента (проф. Сидняев Н. И.)
- Теория меры и ее приложение к теории случайных процессов (проф. Исмагилов Р. С.)
- Обобщенные функции и линейные операторы (доц. Гласко А. В.)
Тематика дипломных работ студентов весьма разнообразна, так как связана с научными интересами руководителей работ – ведущих профессоров и доцентов кафедры.
НАУЧНО-ТЕХНИЧЕСКАЯ КОНФЕРЕНЦИЯ «ВЕСНА» КАФЕДРЫ «ВЫСШАЯ МАТЕМАТИКА»
В середине апреля каждый год кафедра проводит традиционную студенческую научно-техническую конференцию «Весна». С 1987 года бессменным председателем оргкомитета конференции «Весна» является доцент Храпов П. В. Активное участие в конференции принимают зав. кафедрой Сидняев Н. И., проф. Белов В. Н., проф. Исмагилов Р. С., проф. Калинкин А. В., проф. Павлов И. В., проф. Кравченко В. Ф., проф. Васильев Н. С., доц. Гласко А. В., проф. Филиновский А. В., доц. Ветров Л. Г., студенты и аспиранты не только МГТУ им. Н. Э. Баумана, но и многих других ведущих вузов России. Жюри конференции выделяет лучшие доклады и награждает победителей конференции дипломами и ценными подарками (руководитель НУК ФН Назаренко Б. П. и зав. кафедрой «Высшая математика» Сидняев Н. И. принимают живое участие в конференции и выделяют ценные подарки для награждения победителей). Лучшие доклады жюри конференции рекомендует к публикации в ежегодном сборнике тезисов докладов конференции «Весна» МГТУ им. Н.Э.Баумана.
Каждый год кафедра выпускает более 10 дипломированных специалистов, которые безусловно востребованы государственными научно-производственными объединениями, коммерческими структурами и другими организациями и предприятиями. Лучшие выпускники поступают в аспирантуру кафедры «Высшая математика». Некоторые из них стали кандидатами наук и работают на кафедре. С этими молодыми специалистами связано будущее кафедры.
Кафедра ФН-1 «Высшая математика»
В.Я.Томашпольский, Н.Т.Вилисова, А.В.Гласко, С.К.Соболев, Н.И.Сидняев, В.И.Тимонин, Т.Е.Богомолова
Под редакцией Н.И.Сидняева
Набор и верстка: А.И.Петров, К.И.Иванов
Фото: В.Я.Томашпольский



