
Делегация МГТУ им. Н.Э. Баумана и участники Международной конференции «Фундаментальные и прикладные задачи механики» посетили Дом-музей «Усадьба Н.Е. Жуковского»
25 октября представительная делегация МГТУ им. Н.Э. Баумана, в составе которой были деканы факультетов, зав.кафедрой «Теоретическая механика» имени Н.Е. Жуковского, директор музея МГТУ и участники Международной конференции «Фундаментальные и прикладные задачи механики (Fundamental and applied problems of mechanics FAPM-2017)», посвященной 170-летию со дня рождения Николая Егоровича, посетила мемориальный Дом-музей «Усадьба Н.Е. Жуковского» в деревне Орехово Владимирской области - месте проживания семьи основоположника воздухоплавания.
Такие ежегодные встречи давно стали традиционными. В этом году визит был организован в честь юбилея со дня рождения великого русского ученого, профессора нашего университета, долгое время, начиная с конца 1871 года, преподававшего студентам Московского Императорского технического училища, а позже Московского высшего технического училища.
В знак уважения к великому ученому и в память о визите, бауманцы вручили руководителям Музея памятные подарки: портрет Николая Егоровича в полный рост, компьютер и перекидной дисплей с рассказом о нашей кафедре «Теоретической механики имени Н.Е. Жуковского» - единственной кафедре МГТУ им. Н.Э.Баумана, которой присвоено имя.
Фоторепортаж с посещения музея можно посмотреть здесь: http://www.bmstu.ru/mstu/news/?newsid=4522
1847 - 1921
Научная деятельность Н.Е. Жуковского открыла новую страницу в развитии теоретической механики в России, ибо до его работ в российских университетах теоретическая механика даже не рассматривалась как самостоятельная научная дисциплина, а развивалась как прикладная математика. Кафедра теоретической механики Императорского московского технического училища во главе с Н.Е. Жуковским сделалась всероссийской кафедрой механики.
Научное наследие Н.Е. Жуковского огромно. Его исследования охватывали широкую область теоретической и прикладной механики, которые можно классифицировать по основным разделам механики следующим образом: гидромеханика – 46 работ, аэродинамика – 50 работ, теоретическая механика (включая астрономию и математику) – 41 работа, речи и статьи по истории механики – 27, прикладная механика – 30.
Уже в первые годы научной деятельности Н.Е. Жуковский исследовал широкий круг вопросов в области общей механики, механики твердого тела, гидродинамики, астрономии. Он изучал вопрос об ударе твердых тел (1878-1888 гг.), о гироскопических приборах и маятниках (1881-1895 гг.), дал геометрическую интерпретацию общего случая движения твердого тела вокруг неподвижной точки (
Особое место среди его работ по общей механике занимает докторская диссертация «О прочности движения» (
Жуковский был крупным специалистом в России по данному вопросу и был приглашен оппонентом при защите диссертации по устойчивости движения А.М. Ляпуновым.
В
Н.Е. Жуковский выполнил крупные исследования в области гидравлики. Среди этого цикла работ особенно выделяется исследование «О гидравлическом ударе в водопроводных трубах» (
Н.Е. Жуковский занимался также изучением теории смазки и посвятил ей несколько работ.
В
Большую роль здесь сыграло также и знакомство Жуковского с Д.И. Менделеевым. Менделеев был не только великим русским химиком, но и серьезным механиком.
В мировом же масштабе в то время обсуждали проблемы воздухоплавания.
Н.Е. Жуковский с большим интересом прослушал на 6 съезде русских врачей и естествоиспытателей доклад Д.И. Менделеева, относящийся к механике жидкостей и к воздухоплаванию, сопровождавшийся демонстрацией различных моделей.
Профессор Ф.А. Слудский, один из старших коллег Н.Е. Жуковского, тоже интересовался проблемами воздухоплавания.
В
Выяснилась основная задача – установить весь процесс взаимодействия летательного аппарата с воздухом, в частности, научиться вычислять точно подъемную силу.
Н.Е. Жуковский принял решение исследовать всю проблему и разработать методы точных расчетов для решения всех задач, относящихся к развитию аэронавтики.
Особенно велики заслуги Н.Е. Жуковского в области аэромеханики. Именно в области экспериментальной и теоретической аэродинамики Н.Е. Жуковским, справедливо названным В.И. Лениным «отцом русской авиации», достигнуты наиболее важные результаты. Жуковскому здесь принадлежат все основные идеи, остающиеся и в настоящее время руководящими для деятельности ученых и инженеров, работающих в области авиации.
Начав с экспериментальных исследований парения различных моделей, Н.Е. Жуковский в
В
Н.Е. Жуковский создал вихревую теорию гребного винта. На основе этой теории были построены винты Жуковского – «винты НЕЖ».
Все эти работы Н.Е. Жуковского, заложившие основы теоретической аэродинамики, тесно переплетались с практикой авиации и, кроме того, с многочисленными экспериментами.
В области аэродинамики больших скоростей Н.Е. Жуковский написал ряд статей: «Аналогия между движением тяжелой жидкости в узком канале и движением газа в трубе с большой скоростью» (
Н.Е. Жуковский исследовал также вопросы прочности самолета. В
Большое участие принимал Н.Е. Жуковский и в научно-общественной жизни страны. Он участвовал в международных конгрессах, организовывал воздухоплавательные съезды в России, выступал с докладами и публичными лекциями по различным авиационным проблемам. Эти доклады и публичные лекции охотно посещали студенты, молодежь.
Жуковский никогда не был ученым-одиночкой. К научным исследованиям, проводимым в его лаборатории, он смело привлекал студенческую молодежь.
Осенью

Воздухоплавательный кружок
Построить планеры в те годы было довольно трудным делом. Не существовало в тот период никаких норм прочности. Отсутствовали опытные данные о крыльях. Членам кружка приходилось все детали планеров изготовлять собственными руками и многие вопросы, возникавшие при создании планеров, решать буквально на ходу.
Из членов воздухоплавательного кружка впоследствии вышло много выдающихся деятелей советской авиации: А.Н. Туполев, Б.С. Стечкин, Б.Н. Юрьев, В.П. Ветчинкин, А.А. Архангельский, К.А. Ушаков, Г.М. Мусенянц, Г.Х. Сабинин и др.
В своих воспоминаниях о пребывании в Императорском Училище В.П. Ветчинкин особенно выделяет влияние на первоначальное развитие в России авиационной науки и техники Воздухоплавательного кружка МВТУ, в котором начал свою замечательную научную работу и сам В.П. Ветчинкин:
«Зародился кружок в
Сначала в ней были раздвинуты столы, и на освободившемся месте поднялась до потолка ферма ротативной машины Слесарева. Немного позже около окна появился планер, который строили студенты во главе с А.Н. Туполевым, а построив, пробовали летать на нем. Еще немного времени, и освобождается уже половина чертежной, а студент Туполев строит, по указаниям Н.Е. Жуковского, круглую, а затем плоскую аэродинамическую трубу.
Для сбора денег на постройку аэроплана студенты устраивают воздухоплавательную выставку; под нее освобождается уже вся чертежная, и помещение безраздельно переходит в кружок, который, под личным и непосредственным руководством Н.Е. Жуковского и при содействии всеми уважаемого директора училища профессора А.П. Гавриленко, рос и развивался не по дням, а по часам».
Большую роль в дальнейшем развитии русской авиации сыграл XIIВсероссийский съезд естествоиспытателей и врачей (1909-1910 гг.). В работе воздухоплавательной секции, председателем которой был Н.Е. Жуковский, участвовало почти половина всех участником съезда – так был велик в тот период интерес русской общественности к проблемам авиации.
Большую роль в дальнейшем развитии русской авиации сыграл XIIВсероссийский съезд естествоиспытателей и врачей (1909-1910 гг.). В работе воздухоплавательной секции, председателем которой был Н.Е. Жуковский, участвовало почти половина всех участником съезда – так был велик в тот период интерес русской общественности к проблемам авиации.
В результате работы съезда стало очевидно, что дальнейшее развитие авиации зависит в значительной степени от успехов научных исследований в области аэродинамики.
После съезда члены воздухоплавательного кружка МВТУ активно принялись за создание новых, более мощных аэродинамических труб. Не встречая поддержки со стороны царского правительства, они были вынуждены прибегать к организации авиационных выставок, публичных лекций, платных полетов. На собранные средства кружковцы установили в чертежной 5-го курса МВТУ две современные для того времени аэродинамические трубы.

Аэродинамическая труба
Аэродинамическая лаборатория МВТУ была в то время одной из лучших. Она была оборудована новейшей измерительной аппаратурой и моделями, разработанными и построенными руками молодых кружковцев-энтузиастов под руководством Н.Е. Жуковского. За короткий период с 1910 по 1911 гг. в этой лаборатории было проведено свыше 18 научных исследований в области крыльев и воздушных винтов. Экспериментальные работы по аэродинамике, проведенные в лабораториях Училища и Московского университета под руководством Н.Е. Жуковского, оказали огромное влияние на развитие техники аэродинамического эксперимента во всем мире.

Н.Е.Жуковский с учениками возле аэродинамической трубы
Вот как описывает В.П. Ветчинкин свое вступление в члены воздухоплавательного кружка и начало своей работы с Н.Е. Жуковским:
«Началась моя работа в помощь Н.Е. Жуковскому осенью
Для молодого студента работа, которая велась под непосредственным наблюдением такого выдающегося ученого, каким был Н.Е. Жуковский, явилась превосходной школой. Талантливый, чрезвычайно энергичный, В.П. Ветчинкин обратил на себя внимание выдающегося русского ученого. В 1909 году Н.Е. Жуковский начал читать лекции по теоретическим основам воздухоплавания. В.П. Ветчинкин был одним из первых слушателей этих лекций. Он стенографировал эти лекции и готовил их к изданию. Постоянное обсуждение с ним отдельных частей издаваемого курса, а в связи с этим и частные беседы на общенаучные темы как нельзя лучше открывали перед В.П. Ветчинкиным широкие горизонты современной науки.
Лекции Жуковского «Теоретические основы воздухоплавания», записанные и подготовленные к печати В.П. Ветчинкиным, вышли в свет в
Совместная работа по изданию лекций необычайно сблизила учителя и ученика. Для Н.Е. Жуковского его талантливый ученик становится самым близким сотрудником и продолжателем его работы.
Участие в работах кружка, работа по изданию «Теоретических основ воздухоплавания» и возникшее отсюда сближение с Н.Е. Жуковским привело к тому, что В.П. Ветчинкин избирает своей ближайшей специальностью воздухоплавание.
Как отмечал сам В.П. Ветчинкин, с
Вот как Н.Е. Жуковский сам характеризует сотрудничество со своим учеником:
«Начиная с
1 июля
Общее руководство бюро принадлежало Жуковскому, вопросами прочности и расчета винтов руководил Ветчинкин, аэродинамическим расчетом руководил А.Н. Туполев.
Авиационное расчетно-испытательное бюро сыграло исключительную роль в развитии самолетостроения в России. Под руководством Ветчинкина в бюро был проведен расчет нескольких десятков самолетов, в том числе почти всех самолетов русской конструкции.
В.П. Ветчинкин, ясно понимая необходимость систематического изучения поведения самолета в условиях его полета в воздухе, не довольствовался лабораторными и теоретическими исследованиями, он установил прочные связи на аэродроме с летчиками Московской авиационной школы.
С декабря
С началом первой мировой войны при непосредственном участии Н.Е. Жуковского для подготовки военных летчиков создаются четырехмесячные курсы при МВТУ для изучения теоретических основ авиации. Лекции по аэродинамическому расчету самолета и по динамике полета читал сам Н.Е. Жуковский. Для проведения групповых занятий он привлек своих учеников, ставших впоследствии выдающимися авиационными конструкторами: В.П. Ветчинкина, В.С. Кулебакина, Б.С. Стечкина, А.А. Микулина, В.Я. Климова, Г.М. Мусянинца, К.А. Ушакова.

Н.Е.Жуковский и его ближайшие ученики - организаторы и первые руководители основных подразделений ЦАГИ
Лабораторные занятия по аэродинамике со слушателями теоретических курсов велись в аэродинамической лаборатории МВТУ. С помощью военного ведомства ее несколько расширили, построили небольшую специализированную аудиторию с оборудованием для занятий по авиации.
С 1914 по 1917 гг. теоретические авиационные курсы закончило 242 человека – в основном это были студенты МВТУ и Московского университета, из которых впоследствии вышло немало хороших авиационных инженеров и летчиков.
Значительное влияние на развитие аэродинамики имели работы С.А. Чаплыгина, ученика и ближайшего друга Н.Е. Жуковского.
С.А. Чаплыгин работал на кафедре теоретической механики Технического училища с 1896 по 1906 гг.
Замечательные работы С.А. Чаплыгина «Теория решетчатого крыла» (
Можно считать, что в Училище были заложены основы авиационного бомбометания. Н.Е. Жуковский со своими учениками В.П. Ветчинкиным, Б.С. Стечкиным и другими провел большие исследования в этой области. В работах «Бомбометание с аэропланов» (
Н.Е. Жуковский создал блестящую школу учеников в Московском техническом училище, которые превратили молодое училище в первоклассную техническую школу. Они продвинули вперед русскую технику, во многом опередив зарубежные страны.
Среди них должны быть отмечены:
Один из самых знаменитых русских инженеров, почетный академик В.Г. Шухов, который, блестяще сочетая теорию с практикой, был автором смелых и остроумных конструкций, глубоких теоретических исследований, талантливым изобретателем, которого не раз называли русским Эдиссоном.
Инженер Н.П. Зимин, строитель Московского водопровода, много занимавшийся теоретическими исследованиями работы водопровода. Совместно с Н.Е. Жуковским он проводил знаменитые опыты над гидравлическим ударом в водопроводных трубах на Алексеевской водокачке. Во время поездки в Америку Н.П. Зимин своими докладами оказал содействие внедрению теории гидравлического удара в американскую практику.
Инженер А.П. Гавриленко, профессор и директор Технического училища, близкий друг Н.Е. Жуковского, первоклассный конструктор.
Инженер В.И. Гриневецкий, профессор Технического училища, творец русской теплотехнической школы и основатель теплотехнического института, выросший под научным влиянием Н.Е. Жуковского.
Инженер Н.И. Мерцалов, профессор Технического училища, близкий ученик Н.Е. Жуковского, работавший с ним по техническому приложению гидродинамики и теории машин и механизмов.
Инженер А.И. Сидоров, профессор Технического училища, работавший по теории регулирования и особенно способствовавший исследованиям Николая Егоровича по этой теории, а также и по другим вопросам практической механики.
Инженер Л.П. Смирнов, профессор Технического училища, принимавший близкое участие в работах Н.Е. Жуковского по теории регулирования и теории машин.
Инженер С.А. Федоров, профессор Технического училища, который привлек внимание Н.Е. Жуковского к исследованиям по веретенам и другим вопросам текстильных машин и механизмов.
Свою педагогическую деятельность Н.Е. Жуковский начал в
Осенью
В
Жуковский считал для себя великой честью вести преподавание в этих двух крупнейших школах страны. Позднее прибавилась работа в Практической академии коммерческих наук (до
Н.Е. Жуковский принадлежал к числу тех ученых, для которых их творческая научная работа неотделима от преподавания. С самых первых шагов, как учителя физики в гимназии, а затем преподавателя и профессора в Техническом училище и в Московском университете, и до последних дней своей жизни он был неутомимый, аккуратный и прекрасный преподаватель. Постоянное общение с аудиторией, с его учениками на лекциях и в лабораториях, на научных докладах в ученых обществах было для него необходимой частью его научной жизни.
В середине XIX века в Московском университете, Техническом училище, как и во многих других высших учебных заведениях, основное направление в преподавании механики было в основном аналитическое – по Лагранжу. Здесь все изложение ведется чисто аналитическим путем. В предисловии ко 2-му изданию «Аналитической механики» (
Эти курсы, основанные на идеях Лагранжа, были доступны пониманию студентов французской Политехнической школы, обладавших высокой математической подготовкой, но они с трудом усваивались тогдашними студентами Технического училища. Из воспоминаний студента Технического училища, впоследствии почетного академика В.Г. Шухова «до Н.Е. Жуковского механика преподавалась в запутанном и трудном для студентов изложении». (Из материалов музея Н.Е. Жуковского).
В России определяющим было влияние М.В. Остроградского, идеи которого развивал Н.Д. Брашман (1796-1866 гг.) – основатель Московского математического общества. Н.Д. Брашман занимал кафедру механики в Московском университете в течение 30 лет и им заложены первые научные основы этого предмета. Продолжали его работу профессора Ф.А. Слудский и В.Я. Цингер. В то время геометрические идеи Л. Пуансо (1777-1859 гг.) в Московском университете, конечно, были известны, но стояли как-то на втором плане.
Еще будучи студентом Московского университета, Николай Егорович с особым интересом занимался механикой и слушал лекции Слудского и Цингера.
Ф.А. Слудский читал курс механики в течение 20 лет. На этом курсе сказалось влияние Остроградского, Брашмана и Сомова. В предисловии к «Курсу теоретической механики» (М.,
Профессор В.Я. Цингер – геометр по специальности, пользовался особым авторитетом у студентов. Как вспоминал В.В. Голубев, прекрасные лекции Цингера, его геометрический талант, вероятно, в значительной мере определили характер научного мышления Жуковского.
На собрании, посвященном памяти В.Я. Цингера, Н.Е. Жуковский говорил: « … Теперь мы чествуем память математика, которого, по справедливости можно назвать главой русской геометрической школы. Избрав своей специальностью чистую математику, В.Я. Цингер живо интересовался теоретической механикой. Так, в первом томе математического сборника В.Я. Цингер поместил статью «Об относительном движении брошенной точки», в которой замечает, что при обыкновенном приближенном решении этой задачи с помощью теоремы Кориолиса делают собственно неестественное допущение, что точка в своем абсолютном движении находится под эффектом силы, меняющей направление в зависимости от перемещения места наблюдения. Он показывает, что, трактуя задачу, как задачу об абсолютном движении, мы при указанном предположении именно и получаем при переходе к относительному движению интегралы движения в форме Бура. Цингер предлагает задачу об относительном движении брошенной точки решать сначала как задачу об абсолютном движении, отбросив от наблюденной силы тяжести центробежную силу, а потом полученное абсолютное движение преобразовать в относительное. Таким образом получается без всякого интегрирования полное решение задачи.
Своей любовью к образному, геометрическому мышлению В.Я. Цингер увлекал молодых механиков, направляя их труды по тому пути, по которому следовали великие геометры Ньютон, Пуансо, Понселе и Шаль». (Материалы музея Н.Е. Жуковского).
Позднее Н.Е. Жуковский вспоминал: «Мне приятно теперь отметить мои совместные работы с профессорами московского университета, в число которых я имел честь вступить в
Эти два подхода к исследованию задач механики Н.Е. Жуковский оценивал так: «Отстаивая достоинства геометрического метода исследования, я далек от мысли об его исключительности. Механика должна равноправно опираться на анализ и геометрию, заимствуя от них то, что наиболее подходит к существу задачи … Анализ дает нам могущественное оружие для разрешения задач динамики. Но последняя обработка решений задачи всегда будет принадлежать геометрии». (Материалы музея Н.Е. Жуковского).
Можно сказать, что Жуковский произвел революцию в построении и изложении курса механики высшей школы. Вместо изложения теоретической механики в стиле аналитической механики Лагранжа он вводит в механику геометрический метод. Он писал, что «если могут быть споры о самостоятельной роли геометрии при решении недоступных до сих пор задач динамики, то ее высокое значение в преподавании не подлежит сомнению. Ум изучающих весьма часто склонен к формальному изложению. Я из своего педагогического опыта знаю, как часто запоминаются формулы без усвоения стоящих за ними образов. Как это не кажется странным, но одним из затрудняющих вопросов является иногда вопрос о значении той или иной буквы в бойко написанной формуле. В этом отношении геометрическое толкование, предпочтение геометрического толкования аналитическому всегда приносит пользу. Если формулы и подстановки некоторыми из учащихся легко запоминаются, то также скоро исчезают бесследно из памяти, но раз усвоенные геометрические образы, рисующие картину рассматриваемого явления, надолго западают в головы и живут в воображении учащегося». (полн. собр. соч., М., 1937, т.IX, с. 185).
Н.Е. Жуковский подчеркивал в своих лекциях и выступлениях на научных съездах, что «механика развивалась как глубокомысленными трудами аналитиков, так и остроумными исследованиями геометров. При этом часто бывало, что сложные аналитические формулы освещались и представлялись в ясной наглядной форме благодаря удачным геометрическим представлениям. Такие интерпретации охватывали задачу во всей ее полноте и раскрывали многие свойства ее, не замеченные при аналитическом исследовании. Так было с решением задачи о движении твердого тела около его центра тяжести: решение сперва было получено Л. Эйлером аналитическим путем, но оставалось затерянным среди массы формул и только благодаря простым и наглядным интерпретациям Л. Пуансо предстало перед глазами ученых со всей ясностью». (Н.Е. Жуковский. Полн. собр. соч., М., 1937, т. IX, с. 313).
Подчеркивая большое значение геометрических методов исследования в механике, Н.Е. Жуковский говорил о «чувстве меры». Он писал: «Говоря о высоком значении геометрического толкования для преподавания теоретической механики, не скрою, что некоторые авторы геометрией злоупотребляют. Нагромождение кинематических теорем, так же как и нагромождение формул, только запутывает дело преподавания. Геометрическое толкование должно быть ясно и просто и должно всегда близко прилегать к рассматриваемой задаче». (Н.Е. Жуковский. Полн.собр.соч.,
Н.Е. Жуковский считал целесообразным в преподавании широкое развитие лекций. Общеизвестно его высказывание, что по силе впечатления лекционный способ стоит выше других приемов преподавания и ничем не заменим, вместе с тем этот способ есть и самый экономный во времени.
Кроме того, последовательно изложенный курс лекций дает не только фактический материал, который будет спрашиваться на экзаменах, а нечто гораздо более важное – основы современного научного мышления. Если же на процесс высшего образования смотреть как на совокупность подлежащих сдаче экзаменов, то, очевидно, самостоятельная работа студента по учебнику с некоторой помощью «консультантов-репетиторов» полностью решает дело. Однако весь опыт развития высшей школы и в нашей стране, и за рубежом свидетельствует, что слушание лекций выдающихся профессоров имеет какое-то особо ценное значение, представляет важнейший процесс приобщения к творческой деятельности ученого. В лекциях перед слушателями раскрывается как бы лаборатория научного мышления, показывается историческое становления научной истины, выявляются качество мышления лектора и его воззрения на идеалы науки и цель научного мышления. Только на лекциях можно понять сущность той или иной научной школы. Только на лекциях можно услышать оценки новых научных методов исследования и ясно понять, что внес в сокровищницу мировой научной мысли сам лектор, насколько близок ему и плодотворен процесс созидания новых интеллектуальных ценностей. К такому идеалу лекционного преподавания был очень близок Н.Е. Жуковский.
Б.И. Россинский, один из его учеников, позднее писал, что несмотря на отсутствие ораторского искусства и высокий, почти дискантный голос лектора, вся аудитория с напряженным вниманием жадно ловила каждое его слово. Этого Николай Егорович достигал умелой постановкой вопроса, логичностью его изложения, своей исключительной эрудицией. Разрешая один вопрос, он выдвигал новый, заинтересовывал молодежь кажущейся неразрешимостью его. Но знание и логика были на стороне ученого, и как светлели лица студентов, когда мелок Николая Егоровича решал на доске казавшееся неразрешимым. (Воспоминания Б.И. Россинского. Из материалов музея Н.Е. Жуковского).
По понедельникам, четвергам и субботам Н.Е. Жуковский читал лекции в Техническом училище. Курс теоретической механики он разделил на 2 части: первый год читалась так называемая теоретическая механика в составе геометрической статики, геометрической кинематики и начал динамики в элементарном изложении; на втором году читалась аналитическая механика, куда входила аналитическая часть кинематики и полный курс динамики точки и твердого тела вместе с аналитической статикой.
По средам и пятницам – в Московском университете читал механику точки, теорию притяжения, гидромеханику, руководил упражнениями (по 6 часов в день).
Один раз в неделю читал 2-х часовую лекцию в Коммерческой академии на Покровском бульваре.
Курсы, читаемые Н.Е. Жуковским в Техническом училище:
|
Дисциплины |
Годы |
|
1. Математика |
С 01.01.72 – 1885/86 преподаватель математики |
|
2. Теоретическая механика (на механическом и химическом отделениях) |
С 1885 по 1919 (проф. теоретической механики) |
|
3. Упражнения (репетиции) по теоретической механике (на механическом и химическом отделениях) |
Те же |
|
4. Аналитическая механика |
С 14.09.74 по 13.10.79 (доцент) С 13.10.79 по 08.04.87 (сверхштатный профессор)
С 08.04.87 по |
|
5. Упражнения (репетиции) по аналитической механике |
Те же |
|
6. Теория регулирования хода машин |
Специальный курс 1908/09 |
|
7. Воздухоплавание |
Специальный курс с1909/10 по 1916 |
|
8. Гидромеханика |
Специальный курс 1916/17 |
Н.Е. Жуковский выработал прекрасное, ставшее классическим изложение основ теоретической механики, которое было издано в литографированном виде. К этой работе широко привлекались студенты. Так, например, «Аналитическая механика. Лекции проф. Н.Е. Жуковского и Приложение чертежей к Аналитической механике» проф. Н.Е. Жуковского (издано отдельной книжкой) были подготовлены студентом Ф.Ф. Бартом.
Студент В.П. Ветчинкин стенографировал, обработал и издал курс лекций проф. Н.Е. Жуковского по теоретическим основам воздухоплавания. «Прикладная механика». Курс лекций проф. Н.Е. Жуковского (Московская практическая академия коммерческих наук) издал студент В.Н. Владимиров. Лекции по гидродинамике – единственный курс, который был Н.Е. Жуковским напечатан в обработанном виде.
Вот что писал об том курсе академик Л.С. Лейбензон: его курс механики был настолько прост и понятен студентам, что получил распространение по всей России. И только изучив по литографическим запискам курс Н.Е. Жуковского, студенты приступали к изучению трудных курсов своих профессоров. Кафедра теоретической механики Императорского Московского технического училища во главе с Н.Е. Жуковским сделалась всероссийской кафедрой механики. (Лейбензон Л.С. Н.Е. Жуковский (К 100-летию со дня рождения). М-Л., 1947).
После
Жуковский большое внимание уделял частным задачам механики. Академик Л.С. Лейбензон писал, что Н.Е. Жуковский старался выбирать такие задачи, чтобы математический анализ был по возможности прост, и на первый план выступала механическая суть. Задачи, не интересные математически, но важные для техников, представлены очень полно. Разделяя известное высказывание И. Ньютона о том, что «в механике примеры учат не меньше, чем правило», Жуковский вел ежегодно практические занятия со студентами и сам принимал зачеты, требуя, чтобы в специальных тетрадях были представлены подробные решения методически тщательно подобранных задач. (Лейбензон Л.С. Н.Е. Жуковский. М-Л., 1947).
Н.Е. Жуковский считал, что лектор должен руководить практическими занятиями по механике, чтобы иметь возможность проверять усвоение студентами предмета и обеспечить руководство на начальных стадиях обучения.
Н.Е. Жуковский наряду с профессором И.В. Мещерским был одним из пионеров, применившим теоретическую механику к практическим вопросам техники.
Жуковский составлял задачи на специальных карточках, где была сформулирована задача, и был дан ответ.
В Техническом училище были изданы литографическим способом под именем Н.Е. Жуковского и, несомненно, в какой-то степени им авторизованные студенческие издания сборника задач (например, издания 1891, 1907 гг.) и посмертное издание
Б.С. Зернов заменял Н.Е. Жуковского во время болезни. Зернову принадлежат три выпущенные в МВТУ очень ценных задачника по теоретической механике с решениями. Из них особенно важен задачник по кинематике, в котором он, как ассистент Н.Е. Жуковского, собрал очень большое число задач Жуковского на плоское движение, решаемых геометрическими методами.
Перечисленные выше курсы по теоретической, аналитической и прикладной механике неоднократно переиздавались учениками Николая Егоровича.
В полное собрание сочинений Жуковского (Гос.изд.оборон.промышл., М-Л., 1939), изданное под редакцией В.П. Ветчинкина и А.П. Котельникова вошли – лекции, выпуск 4:
Аналитическая механика. Теория регулирования хода машин. Прикладная механика.
Курс лекций (выпуск 5) Н.Е. Жуковский читал в Московском университете с 1886 по 1919 годы:
Кинематика. Статика. Динамика точки (ред. А.П. Котельников).
Лекции по кинематике включают разделы – кинематика точки, сложное движение точки; кинематика неизменяемой системы, сложение движений системы.
В «Кинематике точки» изучается движение точки в естественных осях, в прямоугольных декартовых координатах, в полярных координатах на плоскости, выводятся формулы для проекций скорости и ускорения точки на соответствующие оси, вводятся векторы скорости и ускорения точки.
Для каждого раздела даны подробные примеры.
В примере "даны уравнения движения в смешанных координатах y = at, j = bt"
Здесь y, j – декартова и полярная координаты точки; a, b – постоянные; t – время.
Далее определяется уравнение траектории в полярных координатах
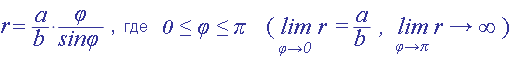
и строится кривая – траектория точки.
Получив зависимость r = r(j), Жуковский доказал возможность и единственность такого задания движения точки.
Теоремы сложения скоростей и ускорений выведены геометрическим методом. Особое внимание Жуковский уделяет вопросу построения Кориолисова (поворотного) ускорения, он излагает способ построения вектора поворотного ускорения, называемый сейчас «правилом Жуковского», которое вошло в современные учебники по теоретической механике.
Кинематика неизменяемой системы включает кинематику простейших движений системы – поступательного и вращательного, кинематику плоскопараллельного, сферического движений, а также общего случая движения системы.
Большое внимание уделено геометрии этих движений. Скорости и ускорения точек в последних двух движениях не рассматриваются.
В разделе «Сложение движений системы» рассматриваются сложение поступательных движений, вращательных движений вокруг пересекающихся и параллельных осей, сложение поступательных и вращательных движений. Все доказательства хорошо иллюстрированы чертежами.
В главе «Аналитическое исследование движений неизменяемой системы» Жуковский получает формулы Эйлера для проекции скорости точки системы при сферическом движении, а также скорости точки неизменяемой системы в общем случае движения путем дифференцирования координатных уравнений. Аналогично, дифференцированием выражений для проекции скорости точки получаются проекции ускорений точки неизменяемой системы (твердого тела) при сферическом движении и в общем случае движения.
Векторные соотношения для ускорения получены как следствия из уравнений проекций ускорений на оси координат.
Здесь же аналитически (с помощью дифференцирования) получены векторные формулы сложения скоростей и ускорений при сложном движении точки. Следует отметить актуальность полученных кинематических соотношений в связи с необходимостью использования ЭВМ для расчетов.
К разделам «Статика» и «Динамика» дано введение, в котором изложены аксиомы динамики и статики. Отметим, что Жуковский вводит теорему параллелограмма сил (а не аксиому) и доказывает ее на основании положений динамики. Кроме того, аксиому

он доказывает, основываясь на законе инерции, кинематических формулах и понятии девиации.
Статика занимает большой объем курса, включает теорию приведения и равновесия сходящихся и параллельных сил, много места уделено определению центров тяжестей конкретных тел, изложена теория моментов силы, доказана теорема: «Пара не имеет равнодействующей», изложена теория пар сил, доказана основная теорема статики.
В главе «О равновесии» доказаны условия равновесия различных систем сил, приведены примеры равновесия тел под действием плоской и пространственной систем сил.
Завершается курс теоретической механики разделом «Динамика точки». Выводятся уравнения движения точки в инерциальной системе отсчета, рассматриваются различные виды дифференциальных уравнений для свободной точки и методы их интегрирования. Решаются задачи о прямолинейном и криволинейном движениях точки, многие эти задачи вошли сейчас в известные задачники.
Выводятся общие теоремы динамики для материальной точки, рассматривается движение точки под действием центральной силы, рассматривается теория потенциального поля, большое место уделено задачам о движении планет.
Завершается раздел главой о равновесии и движении несвободной материальной точки. Выводятся дифференциальные уравнения движения точки по гладкой поверхности и линии. Определяется давление точки на опору, решены задачи о движении математического маятника. Выводятся дифференциальные уравнения относительного движения материальной точки, решается ряд задач на эту тему.
Курс «Аналитическая механика» Николай Егорович читал в МВТУ с 1874 по 1920 гг. (свыше 40 лет). Этот курс видоизменялся и совершенствовался на протяжении времени, учитывая потребности практики (техники). Основное содержание курса сложилось к концу 19-го века и все издания после
Курс содержит разделы – кинематика точки и системы, динамика и статика свободной и несвободной точки, динамика и статика механической системы, ньютоновский удар, применение метода Лагранжа к задачам на упругие системы.
Раздел «Кинематика точки» изложен компактно, содержит четкое разбиение по параграфам, в которых излагаются способы задания движения точки; все положения четко доказаны. Кинематика системы включает формулы Эйлера для проекций скорости точки твердого тела, вращающегося около неподвижной точки на прямоугольные оси координат, имеющие начало в этой же неподвижной точке; формулы для «скорости точки свободного твердого тела»; «теорему Кориолиса и аналитическое выражение проекций поворотного ускорения». Здесь же содержится правило для построения поворотного ускорения (правило Жуковского). Отметим, что Жуковский определял направление вектора угловой скорости так, чтобы наблюдатель, из конца вектора в его начало, видел вращение тела совершающимся по часовой стрелке (а не против часовой стрелки).
Раздел «Динамика точки» построен во многом так же, как и в Лекциях, вып. 5, но в «Аналитической механике» более четкое разбиение раздела на подразделы (движение планет, равновесие несвободной материальной точки, движение несвободной материальной точки, об относительном движении материальной точки), а также даны примеры их технического приложения.
Излагая «Статику системы», Жуковский вводит определение механической системы, определение связи, проводит классификацию связей и вводит понятие числа степеней свободы механической системы, дает определение возможного перемещения точки, очень подробно излагает доказательство принципа Лагранжа (о равновесии системы) методом Ампера, добиваясь доказательства принципа «во всей полноте», рассматривает равновесие гибкой нити.
«Динамика системы» начинается с «принципа Даламбера» и общего уравнения динамики, здесь же излагается запись общего уравнения динамики в обобщенных координатах и условия равновесия (или движения) в обобщенных координатах (дифференциальные уравнения движения).
Общие теоремы динамики выводятся из общего уравнения динамики системы.
«Теорема о движении центра тяжести» (центра масс) изложена с различными частными случаями, подробно описано действие прибора Теплера, наглядно показывающего, что «внутренние силы, вызывающие относительное перемещение частей системы, не могут привести в движение ее центр тяжести или изменить его движение».
Теорема об изменении кинетического момента системы и законы сохранения кинетического момента также проиллюстрированы глубокими примерами. Разобрана теория движения человека на вращающейся скамье при наличии начальной угловой скорости системы человек-скамья (w0) . Естественно, что с увеличением момента инерции системы человек-скамья относительно оси вращения (руки человека разведены в стороны) Jz , угловая скорость системы уменьшается
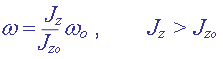
Указано на ошибку Delaynay, объясняется, что если нет начальной угловой скорости системы человек-скамья, то по теореме площадей имеем
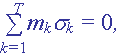
где mk, sk – масса и площадь, ометаемая радиусом-вектором k-той точки.
Жуковский объяснил, что если человек рукой ометает некоторую площадь в плоскости, перпендикулярной оси вращения, то скамья с человеком вокруг своей оси повернется на некоторый угол в сторону, противоположную движению руки.
Теорема об изменении кинетической энергии доказана в дифференциальной и интегральной формах, введено понятие потенциальной энергии и получен закон сохранения механической энергии.
Геометрия масс, теория главных осей инерции тела, динамическое уравновешивание вращающегося тела изложены полно, выведены динамические уравнения вращательного и плоскопараллельного движения твердого тела.
Решены задачи о движении физического маятника вокруг неподвижной и совершающей возвратно-поступательное движение горизонтальной оси. Первая иллюстрирует использование уравнения вращательного движения, вторая посвящена теории вынужденных колебаний системы с кинематическим (инерционным) возбуждением. Даны другие примеры применения уравнений динамики системы к решению задач.
Добавление приложения метода Лагранжа к задачам строительной механики было сделано в 1910 году. Здесь даются «приемы решения задач на неопределенно- статические системы, исследование которых часто затрудняет конструкторов».
Курс «Теория регулирования хода машин» Н.Е. Жуковский прочел в 1908-1909 учебном году студентам МВТУ. Появился в печати в
Курс лекций «Прикладная механика» читался Жуковским в Московской практической академии коммерческих наук и был издан в
Здесь не касаемся других читаемых Н.Е. Жуковским курсов. Рассмотренные выше учебные курсы настолько полны и хорошо написаны, что вполне составляют конкуренцию современным курсам по механике с точки зрения объема излагаемого материала, качества изложения, разносторонности подготовки и высокой научной квалификации автора.
В предисловии редакции (ГИОП, М-Л.,
Николай Егорович сопровождал свои лекции и практические занятия иллюстрациями положений механики на специальных приборах, иллюстрировал задачи моделями механизмов, старался привить выпускникам МВТУ инженерные навыки. Им и его учениками была создана коллекция приборов Жуковского на кафедре «Теоретическая механика».
Во многих разделах своих классических курсов он находил новые подходы к изложению материала, свои механические трактовки теорем, следствий из теорем, критически анализировал научные материалы других ученых, приводил практические примеры.
Научные работы Н.Е. Жуковского по теоретической и аналитической механике внесли существенный вклад в развитие механики и являлись источником развития читаемых им лекционных курсов.
Жуковским написано 68 работ по теоретической и прикладной механике (включая работы по астрономии и прикладной математике). Здесь отметим некоторые работы Жуковского по теоретической и аналитической механике.
Ряд ранних работ посвящен соударению тел («О соударении тел»
В курс аналитической механики Н.Е. Жуковского включен раздел о равновесии гибкой нити.
Есть у него и весьма интересная исследовательская статья «Связь между вопросами о движении материальной точки и о равновесии гибкой нити» (
Н.Е. Жуковский провозгласил идею добротного политехнического образования, в котором главное – сочетание высокого уровня теоретической подготовки с привитием навыков решения практических задач и с анализом геометрии движения, наглядностью и простотой представления движения механических систем.
Этой идее посвящена его статья «О значении геометрического истолкования в теоретической механике» (Матем.сборн., 1896, т. 18, вып. 1). В этом же году он опубликовал статью «Геометрическая интерпретация рассмотренного С.В. Ковалевской случая движения тяжелого твердого тела около неподвижной точки». В ней проведен тщательный анализ общих свойств движения тела с одной неподвижной точкой в случае, который был открыт Ковалевской в 1888 году. Сейчас уже этот классический материал вошел в учебники. В
В России 18 и 19-го веков сложилась школа механики – школа Остроградского, основным принципом которой является сознательное сочетание теории с практикой. Преподавание механики Жуковским в Московском университете также было подчинено этому принципу. В статье «Механика в Московском университете за последнее пятидесятилетие» (
Николай Егорович глубоко понимал механику, ее основы, изучал труды классиков механики, труды других ученых механиков. Немало работ Жуковского посвящено глубокому анализу научных трудов ряда ученых.
Н.Е. Жуковским написаны статьи: «Ньютон как основатель теоретической механики» (В кн. Двухсотлетие памяти Ньютона (1687-1887). М., 1888, с. 13-20, «О трудах С.В. Ковалевской по прикладной математике». Матем.сб., 1891, т. 16, вып. 1, с. 10-20).
Николай Егорович в статье «Ученые труды М.В. Остроградского по механике» (Матем.сб., 1902, т. 22, с. 533-573) сделал обзор работ основателя школы русской механики.
Позднее им была написана статья «О работах В.Я Цингера по механике» (Матем.сб., 1911, т. 28, вып. 1, с. 50-53).
Все эти работы говорят о том, как глубоко вникал Жуковский в суть задачи механики, как хорошо был знаком с работами классиков механики и крупных механиков.
Научные работы Николая Егоровича питали его педагогическую деятельность, позволяли во всех тонкостях разбирать основные положения механики и рассматривать ее приложение к конкретным практическим задачам. Такое исключительное сочетание научной, учебной и практической деятельности привлекало множество студентов, которые постоянно обращались к Жуковскому за практическим советом и работали с ним и после окончания училища.
Фотографии с похорон Н.Е. Жуковского
http://www.fn.bmstu.ru/faculty-basic-sciences/news-and-events-fs/item/672-visit-to-the-house-museum-n-zhukovsky-fs-ru#sigProIdc470b46bf9





